Đề thi vào 10 môn Toán Cần Thơ năm 2018

Đề bài

Câu 1 (1,0 điểm). Giải phương trình và hệ phương trình sau:

a) $2{x^2} - 3x - 2 = 0$                                                                                 b)  $\left\{ \begin{array}{l}2x - 3y = 12\\3x + y = 7\end{array} \right.$

Câu 2 (1,0 điểm).

a) Rút gọn biểu thức $A = \sqrt {9 - 4\sqrt 5 }  + \dfrac{1}{{\sqrt 5  - 2}}$

b) Vẽ đồ thị của hàm số $y = \dfrac{3}{4}{x^2}.$

Câu 3 (1,5 điểm):

a) Khi thực hiện xây dựng trường điển hình đổi mới năm 2017, hai trường trung học cơ sở A và B có tất cả 760 học sinh đăng ký tham gia nội dung hoạt động trải nghiệm. Đến khi tổng kết, số học sinh tham gia đạt tỷ lệ 85% so với số đã đăng ký. Nếu tính riêng thì tỷ lệ học sinh tham gia của trường A và trường B lần lượt là 80% và 89,5%. Tính số học sinh ban đầu đăng ký tham gia của mỗi trường.

b) Tìm tất cả các giá trị của tham số $m$ sao cho phương trình $2{x^2} - \left( {m + 5} \right)x - 3{m^2} + 10m - 3 = 0$ có hai nghiệm phân biệt ${x_1},\;\;{x_2}$ thỏa mãn $x_1^2 + x_2^2 - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4.$

Câu 4 (2,5 điểm):

Cho đường tròn tâm O và điểm P nằm ngoài (O). Vẽ tiếp tuyến PC của (O) (C là tiếp điểm) và cát tuyến PAB (PA < PB) sao cho các điểm A, B, C nằm cùng phía so với đường thẳng PO. Gọi M là trung điểm của đoạn AB và CD là đường kính của (O).

a) Chứng minh tứ giác PCMO là tứ giác nội tiếp.

b) Gọi E là giao điểm của đường thẳng PO với đường thẳng BD. Chứng minh AM.DE = AC.DO.

c) Chứng minh đường thẳng CE vuông góc với đường thẳng CA.

Lời giải chi tiết

PHẦN 1. TRẮC NGHIỆM

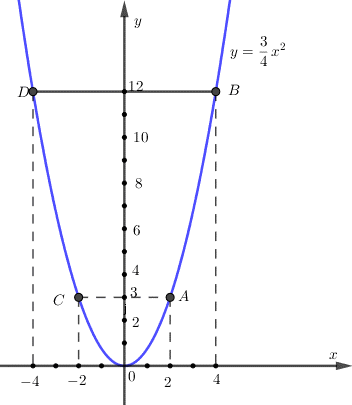
PHẦN 2: TỰ LUẬN

Câu 1

Phương pháp:

Sử dụng công thức nghiệm để giải phương trình bậc hai.

Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.

Cách giải:

a) $2{x^2} - 3x - 2 = 0$

Ta có: $\Delta  = {\left( { - 3} \right)^2} - 4.2.\left( { - 2} \right) = 25 > 0$

Nên phương trình đã cho có hai nghiệm phân biệt: $\left[ \begin{array}{l}{x_1} = \dfrac{{3 - 5}}{{2.2}} = \dfrac{{ - 1}}{2}\\{x_2} = \dfrac{{3 + 5}}{{2.2}} = 2\end{array} \right.$

Vậy tập nghiệm của phương trình đã cho là: $S = \left\{ { - \dfrac{1}{2};2} \right\}$ .

b) $\left\{ \begin{array}{l}2x - 3y = 12\\3x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 3y = 12\\9x + 3y = 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}11x = 33\\y = 7 - 3x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 7 - 3.3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y =  - 2\end{array} \right.$

Vậy hệ phương trình đã cho có 1 nghiệm duy nhất là: $\left( {x;y} \right) = \left( {3; - 2} \right)$

Câu 2

Phương pháp:

+) Sử dụng công thức $\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\;\;khi\;\;\;A \ge 0\\ - A\;\;khi\;\;A < 0\end{array} \right.$ và trục căn thức ở mẫu.

+) Lập bảng giá trị các điểm thuộc đồ thị hàm số sau đó vẽ đồ thị hàm số.

Cách giải:

a) Rút gọn biểu thức $A = \sqrt {9 - 4\sqrt 5 }  + \dfrac{1}{{\sqrt 5  - 2}}$

$\begin{array}{l}A = \sqrt {9 - 4\sqrt 5 }  + \dfrac{1}{{\sqrt 5  - 2}}\\ = \sqrt {{2^2} - 2.2.\sqrt 5  + {{\left( {\sqrt 5 } \right)}^2}}  + \dfrac{{\sqrt 5  + 2}}{{\left( {\sqrt 5  - 2} \right)\left( {\sqrt 5  + 2} \right)}}\\ = \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}}  + \dfrac{{\sqrt 5  + 2}}{{5 - 4}}\\ = \left| {2 - \sqrt 5 } \right| + \sqrt 5  + 2\\ = \sqrt 5  - 2 + \sqrt 5  + 2\left( {\,Do\,\,\,2 - \sqrt 5  < 0} \right)\\ = 2\sqrt 5 \end{array}$

b) Vẽ đồ thị của hàm số $y = \dfrac{3}{4}{x^2}.$

Bảng giá trị

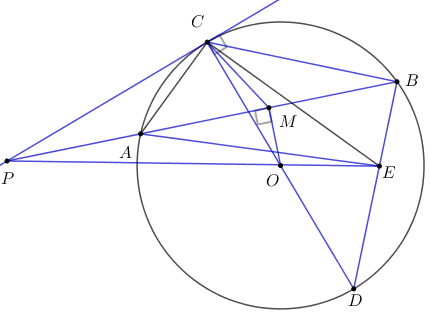
Khi đó đồ thị hàm số đã cho  là 1 đường cong và đi qua các điểm $A\left( {2;3} \right);B\left( {4;12} \right);C\left( { - 2;3} \right);D\left( { - 4;12} \right);O\left( {0;0} \right)$

Câu 3

Phương pháp:

a) Giải bài toán bằng cách lập phương trình.

b) Tìm điều kiện của m để phương trình có hai nghiệm phân biệt sau đó áp dụng định lý Vi-ét để làm bài.

Cách giải:

a) Khi thực hiện xây dựng trường điển hình đổi mới năm 2017, hai trường trung học cơ sở A và B có tất cả 760 học sinh đăng ký tham gia nội dung hoạt động trải nghiệm. Đến khi tổng kết, số học sinh tham gia đạt tỷ lệ 85% so với số đã đăng ký. Nếu tính riêng thì tỷ lệ học sinh tham gia của trường A và trường B lần lượt là 80% và 89,5%. Tính số học sinh ban đầu đăng ký tham gia của mỗi trường.

Gọi số học sinh trường A đăng ký hoạt động là $x$ (học sinh), $\left( {x < 760,\;x \in {N^*}} \right).$

Gọi số học sinh trường B đăng ký hoạt động là $y$ (học sinh), $\left( {y < 760,\;y \in {N^*}} \right).$

Khi đó tổng số học sinh hai trường đăng kí là: $x + y = 760.\;\;\;\;\;\;\left( 1 \right)$

Số học sinh hai trường tham gia là: $760.\dfrac{{85}}{{100}} = 646$ (học sinh).

Số học sinh trường A tham gia là: $80\% x = \dfrac{4}{5}x$ (học sinh).

Số học sinh trường B tham gia là: $89,5\% y = \dfrac{{179}}{{200}}y$ (học sinh).

Theo đề bài ta có phương trình: $\dfrac{4}{5}x + \dfrac{{179}}{{200}}y = 646\;\;\;\left( 2 \right).$

Từ (1) và (2) ta có hệ phương trình: $\left\{ \begin{array}{l}x + y = 760\\\dfrac{4}{5}x + \dfrac{{179}}{{200}}y = 646\end{array} \right.$

$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + y = 760\\160x + 179y = 129200\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}160x + 160y = 121600\\160x + 179y = 129200\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}19y = 7600\\x = 760 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 400\;\;\;\left( {tm} \right)\\x = 360\;\;\left( {tm} \right)\end{array} \right..\end{array}$

Vậy ban đầu trường A có 360 học sinh đăng ký, trường B có 400 học sinh đăng ký.

b) Tìm tất cả các giá trị của tham số $m$ sao cho phương trình $2{x^2} - \left( {m + 5} \right)x - 3{m^2} + 10m - 3 = 0$ có hai nghiệm phân biệt ${x_1},\;\;{x_2}$ thỏa mãn $x_1^2 + x_2^2 - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4.$

Phương trình có hai nghiệm phân biệt ${x_1},\;{x_2} \Leftrightarrow \Delta  > 0$

$\begin{array}{l} \Leftrightarrow {\left( {m + 5} \right)^2} - 4.2\left( { - 3{m^2} + 10m - 3} \right) > 0\\ \Leftrightarrow {m^2} + 10m + 25 + 24{m^2} - 80m + 24 > 0\\ \Leftrightarrow 25{m^2} - 70m + 49 > 0\\ \Leftrightarrow {\left( {5m - 7} \right)^2} > 0\\ \Leftrightarrow m \ne \dfrac{7}{5}\end{array}$

Với $m \ne \dfrac{7}{5}$ thì phương trình đã cho có hai nghiệm phân biệt ${x_1},\;{x_2}.$

Áp dụng hệ thức Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{m + 5}}{2}\\{x_1}{x_2} = \dfrac{{ - 3{m^2} + 10m - 3}}{2}\end{array} \right..$

Theo đề bài ta có: $x_1^2 + x_2^2 - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4$

$\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - \left( {{x_1} + {x_2}} \right) - {x_1}{x_2} = 4\\ \Leftrightarrow {\left( {\dfrac{{m + 5}}{2}} \right)^2} - \left( {\dfrac{{m + 5}}{2}} \right) - \dfrac{{ - 3{m^2} + 10m - 3}}{2} = 4\\ \Leftrightarrow {\left( {m + 5} \right)^2} - 2\left( {m + 5} \right) + 2\left( {3{m^2} - 10m + 3} \right) = 16\\ \Leftrightarrow 7{m^2} - 12m + 5 = 0\\ \Leftrightarrow \left( {7m - 5} \right)\left( {m - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}7m - 5 = 0\\m - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{5}{7}\;\;\left( {tm} \right)\\m = 1\;\;\;\;\left( {tm} \right)\end{array} \right..\end{array}$

Vậy $m = \dfrac{5}{7}$ hoặc $m = 1$ thỏa mãn bài toán.

Câu 4

Phương pháp:

+) Chứng minh tứ giác nội tiếp dựa vào các dấu hiệu nhận biết.

+) Chứng minh các cặp tam giác đồng dạng tương ứng sau đó suy ra tỉ lệ cần chứng minh.

Cách giải:

Cho đường tròn tâm O và điểm P nằm ngoài (O). Vẽ tiếp tuyến PC của (O) (C là tiếp điểm) và cát tuyến PAB (PA < PB) sao cho các điểm A, B, C nằm cùng phía so với đường thẳng PO. Gọi M là trung điểm của đoạn AB và CD là đường kính của (O).

a) Chứng minh tứ giác PCMO là tứ giác nội tiếp.

Ta có $M$ là trung điểm của $AB\;\left( {gt} \right) \Rightarrow OM \bot AB$ (tính chất đường kính và dây cung)

$\Rightarrow \widehat {AMO} = \widehat {PMO} = {90^0}.$

Có $PC$ là tiếp tuyến của (O) tại C $\Rightarrow \widehat {PCO} = {90^0}.$

Xét tứ giác $PCMO$ ta có: $\widehat {PMO} = \widehat {PCO} = {90^0}\;\;\left( {cmt} \right)$

Mà C và M là 2 đỉnh kề nhau cùng nhìn cạnh PC dưới 1 góc vuông$\Rightarrow PCMO$ là tứ giác nội tiếp (dấu hiệu nhận biết tứ giác nội tiếp).

b) Gọi E là giao điểm của đường thẳng PO với đường thẳng BD. Chứng minh AM.DE = AC.DO.

Vì tứ giác $PCMO$ là tứ giác nội tiếp $\Rightarrow \widehat {POC} = \widehat {PMC}$ (cùng chắn cung $PC$)

Mà $\widehat {DOE} = \widehat {POC}$ (hai góc đối đỉnh)

$\Rightarrow \widehat {DOE} = \widehat {AMC}\;\;\left( { = \widehat {POC}} \right).$

Xét tam giác: $\Delta ACM$ và $\Delta DEO$ ta có:

$\widehat {DOE} = \widehat {AMC}\;\left( {cmt} \right)$

$\widehat {ODE} = \widehat {CAM}$ (hai góc nội tiếp cùng chắn cung $BC$ của đường tròn (O))

$\begin{array}{l} \Rightarrow \Delta ACM \sim \Delta DEO\;\left( {g - g} \right)\\ \Rightarrow \dfrac{{AC}}{{DE}} = \dfrac{{AM}}{{DO}} \Rightarrow AC.DO = AM.DE\;\;\left( {dpcm} \right).\end{array}$

c) Chứng minh đường thẳng CE vuông góc với đường thẳng CA.

Ta có: $\Delta ACM \sim \Delta DEO\;\left( {cmt} \right)$

$\Rightarrow \dfrac{{DE}}{{AC}} = \dfrac{{OD}}{{AM}} = \dfrac{{2OD}}{{2AM}} = \dfrac{{CD}}{{AB}}.$

Xét $\Delta DEC$ và $\Delta ACB$ ta có:

$\dfrac{{DE}}{{AC}} = \dfrac{{DC}}{{AB}}\;\;\left( {cmt} \right)$

$\widehat {EDC} = \widehat {BAC}$  (hai góc nội tiếp cùng chắn cung $BC$)

$\Rightarrow \Delta DEC \sim \Delta ACB\;\left( {c - g - c} \right).$

$\Rightarrow \widehat {DCE} = \widehat {CBA}$ (hai góc tương ứng).

Lại có: $\widehat {CBA} = \widehat {PCA}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung $CA$)

$\Rightarrow \widehat {DCE} = \widehat {PCA}\;\;\left( { = \widehat {CBA}} \right).$

Mặt khác: $\widehat {PCA} + \widehat {ACO} = {90^0}\;\;\left( {gt} \right)$ (PC là tiếp tuyến của đường tròn tại C)

$\begin{array}{l} \Rightarrow \widehat {DCE} + \widehat {ACO} = {90^0}\;\;hay\;\;\widehat {ACE} = {90^0}.\\ \Rightarrow AC \bot CE\;\;\left( {dpcm} \right).\end{array}$