Đề thi vào 10 môn Toán Đắk Nông năm 2020Tải vềBài 1: a) Gọi
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Bài 1: a) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 3x + 2 = 0.\) Tính tổng \(S = {x_1} + {x_2}\) và \(P = {x_1}{x_2}.\) b) Giải phương trình \({x^2} - x + 5 = {x^2} + 2x - 1.\) c) Giải hệ phương trình: \(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right..\) Bài 2: Cho biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 0,\,\,x \ne 4\). a) Rút gọn biểu thức A. b) Tìm tất cả các giá trị của x để \(A > 1\). Bài 3: a) Vẽ parabol \(\left( P \right):\,\,y = 2{x^2}\). b) Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\), (\(m\) là tham số). Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\). Bài 4: Cho \(\Delta ABC\) có ba góc nhọn. Hai đường cao của \(\Delta ABC\) là \(AD,\,\,BE\) cắt nhau tại \(H\,\,\,\left( {D \in BC,\,\,\,E \in AC} \right).\) a) Chứng minh \(CDHE\) là tứ giác nội tiếp một đường tròn. b) Chứng minh \(HA.HD = HB.HE.\) c) Gọi điểm \(I\)là tâm đường tròn ngoại tiếp tứ giác \(CDHE.\) Chứng minh \(IE\) là tiếp tuyến của đường tròn đường kính \(AB.\) Bài 5: Cho các số thực dương \(x,\,\,y > 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\) Lời giải Bài 1 (2 điểm): Cách giải: a) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 3x + 2 = 0.\) Tính tổng \(S = {x_1} + {x_2}\) và \(P = {x_1}{x_2}.\) Phương trình \({x^2} - 3x + 2 = 0\) có: \(a + b + c = 1 - 3 + 2 = 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \dfrac{c}{a} = 2\end{array} \right..\) Khi đó ta có: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = 1 + 2 = 3\\P = {x_1}{x_2} = 1.2 = 2\end{array} \right..\) Vậy \(S = 3,\,\,P = 2.\) b) Giải phương trình \({x^2} - x + 5 = {x^2} + 2x - 1.\) \(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} - x + 5 = {x^2} + 2x - 1\\ \Leftrightarrow 2x + x = 5 + 1\\ \Leftrightarrow 3x = 6\\ \Leftrightarrow x = 2.\end{array}\) Vậy tập nghiệm của phương trình là: \(S = \left\{ 2 \right\}.\) c) Giải hệ phương trình: \(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right..\) \(\left\{ \begin{array}{l}4x - 3y = - 10\\x + 2y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 3y = - 10\\4x + 8y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}11y = 22\\x = 3 - 2y\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 3 - 2.\left( { - 2} \right) = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 2\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( { - 1;\,\,2} \right).\) Bài 2 (2,0 điểm) Cách giải: Cho biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 0,\,\,x \ne 4\). a) Rút gọn biểu thức A. Với \(x \ge 0,\,\,x \ne 4\) ta có: \(\begin{array}{l}A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\\A = \dfrac{x}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\\A = \dfrac{{x + \sqrt x + 2 + \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{x + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\A = \dfrac{{\sqrt x }}{{\sqrt x - 2}}\end{array}\) b) Tìm tất cả các giá trị của x để \(A > 1\). Ta có: \(\begin{array}{l}\,\,\,\,\,A > 1\\ \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x - 2}} > 1\\ \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x - 2}} - 1 > 0\\ \Leftrightarrow \dfrac{{\sqrt x - \sqrt x + 2}}{{\sqrt x - 2}} > 0\\ \Leftrightarrow \dfrac{2}{{\sqrt x - 2}} > 0\\ \Leftrightarrow \sqrt x - 2 > 0\\ \Leftrightarrow \sqrt x > 2\\ \Leftrightarrow x > 4\end{array}\) Kết hợp điều kiện xác định ta có \(x > 4\) thỏa mãn. Vậy để \(A > 1\) thì \(x > 4\). Bài 3 (2,0 điểm) Cách giải: a) Vẽ parabol \(\left( P \right):\,\,y = 2{x^2}\). Ta có bảng giá trị:
Do đó, parabol \(\left( P \right):\,\,\,y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;8} \right)\), \(\left( { - 1;2} \right)\), \(\left( {0;0} \right)\), \(\left( {1;2} \right)\), \(\left( {2;8} \right)\) và nhận \(Oy\) làm trục đối xứng. Đồ thị hàm số:
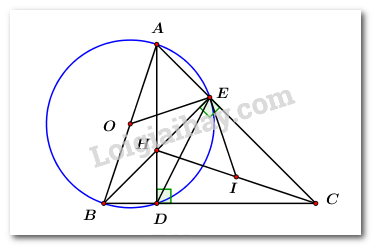
b) Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\), (\(m\) là tham số). Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10\). Để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 1 = 0\) (*) có 2 nghiệm phân biệt \({x_1},\,\,{x_2}\) thì: \(\begin{array}{l}\,\,\,\,\,\,\Delta ' > 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} - 3m + 1 > 0\\ \Leftrightarrow {m^2} + 2m + 1 - {m^2} - 3m + 1 > 0\\ \Leftrightarrow - m + 2 > 0\\ \Leftrightarrow m < 2\end{array}\) Khi đó, áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2\\{x_1}{x_2} = {m^2} + 3m - 1\end{array} \right.\). Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,x_1^2 + x_2^2 = 10\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow {\left( {2m + 2} \right)^2} - 2\left( {{m^2} + 3m - 1} \right) = 10\\ \Leftrightarrow 4{m^2} + 8m + 4 - 2{m^2} - 6m + 2 = 10\\ \Leftrightarrow 2{m^2} + 2m - 4 = 0\\ \Leftrightarrow {m^2} + m - 2 = 0\\ \Leftrightarrow {m^2} - m + 2m - 2 = 0\\ \Leftrightarrow m\left( {m - 1} \right) + 2\left( {m - 1} \right) = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 2\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\) Vậy \(m = 1\) hoặc \(m = - 2\). Bài 4 (3 điểm): Cách giải: Cho \(\Delta ABC\) có ba góc nhọn. Hai đường cao của \(\Delta ABC\) là \(AD,\,\,BE\) cắt nhau tại \(H\,\,\,\left( {D \in BC,\,\,\,E \in AC} \right).\)
a) Chứng minh \(CDHE\) là tứ giác nội tiếp một đường tròn. Ta có: \(AD,\,\,BE\) là hai đường cao của \(\Delta ABC\) (gt) \( \Rightarrow \left\{ \begin{array}{l}AD \bot BC = \left\{ D \right\}\\BE \bot AC = \left\{ E \right\}\end{array} \right.\) \( \Rightarrow \angle ADC = \angle BEC = {90^0}\) Xét tứ giác \(CDHE\) ta có: \(\angle HDC + \angle HEC = {90^0} + {90^0} = {180^0}\) Mà hai góc này là hai góc đối diện \( \Rightarrow \angle CDHE\) là tứ giác nội tiếp. (dhnb) b) Chứng minh \(HA.HD = HB.HE.\) Xét \(\Delta HAE\) và \(\Delta HBD\) ta có: \(\angle AHE = \angle BHD\) (hai góc đối đỉnh) \(\begin{array}{l}\angle AEH = \angle BDH = {90^0}\\ \Rightarrow \Delta AHE \sim \Delta BHD\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{AH}}{{BH}} = \dfrac{{HE}}{{HD}} \Rightarrow AH.DH = BH.EH\,\,\,\left( {dpcm} \right).\end{array}\) c) Gọi điểm \(I\)là tâm đường tròn ngoại tiếp tứ giác \(CDHE.\) Chứng minh \(IE\) là tiếp tuyến của đường tròn đường kính \(AB.\) Xét tứ giác \(ABDE\) ta có: \(\angle ADB = \angle AEB = {90^0}\) Mà hai đỉnh \(D,\,\,E\) là hai đỉnh liên tiếp của tứ giác \( \Rightarrow \angle ABDE\) là tứ giác nội tiếp. (dhnb) Lại có: \(\Delta AEB\) vuông tại \(E.\) \( \Rightarrow A,\,\,B,\,\,D,\,\,E\) cùng thuộc đường tròn tâm \(O\) đường kính \(AB.\) Ta có: \(ABDE\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle EDC = \angle BAE\) (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện). (1) Ta có: \(I\) là tâm đường tròn ngoại tiếp tứ giác \(CDHE\) \( \Rightarrow I\) là trung điểm của \(HC.\) \(\Delta ECH\) vuông tại \(E\) có đường trung tuyến \(EI\) \( \Rightarrow EI = HI = \dfrac{1}{2}HC\) (đường trung tuyến ứng với cạnh huyền của tam giác vuông) \( \Rightarrow \Delta HEI\) cân tại \(I\) \( \Rightarrow \angle IEH = \angle IHE\) (tính chất tam giác cân) Hay \(IEH = \angle EHC\) (2) Tứ giác \(CDHE\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle CDE = \angle CHE\) (hai góc nội tiếp cùng chắn cung \(EC\)) (3) Từ (1), (2) và (3) suy ra: \(\angle EDC = \angle BAE = \angle HEI\) \(\Delta AOE\) cân tại \(O\,\,\left( {OA = OE} \right)\) \( \Rightarrow \angle OEB = \angle OBE\) (tính chất tam giác cân) Hay \(\angle BAE = \angle OEA\) Mà \(\angle OBE + \angle BAE = {90^0}\) \( \Rightarrow \angle OEB + \angle HEI = {90^0}\) Hay \(OE \bot EI\) \( \Rightarrow EI\) là tiếp tuyến của đường tròn đường kính\(AB.\) (đpcm) Bài 5 (1,0 điểm) Cách giải: Cho các số thực dương \(x,\,\,y > 1\). Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\). Áp dụng BĐT Cô-si t có: \(\begin{array}{l}x = x - 1 + 1 \ge 2\sqrt {\left( {x - 1} \right).1} = 2\sqrt {x - 1} \\ \Rightarrow {x^2} \ge 4\left( {x - 1} \right)\\ \Rightarrow \dfrac{{{x^2}}}{{y - 1}} \ge \dfrac{{4\left( {x - 1} \right)}}{{y - 1}}\end{array}\) Tương tự ta có: \(\dfrac{{{y^2}}}{{x - 1}} \ge \dfrac{{4\left( {y - 1} \right)}}{{x - 1}}\). Khi đó ta có: \(\begin{array}{l}P = \dfrac{{{x^2}}}{{y - 1}} + \dfrac{{{y^2}}}{{x - 1}}\\\,\,\,\,\, \ge \dfrac{{4\left( {x - 1} \right)}}{{y - 1}} + \dfrac{{4\left( {y - 1} \right)}}{{x - 1}}\\\,\,\,\, \ge 2\sqrt {\dfrac{{4\left( {x - 1} \right)}}{{y - 1}}.\dfrac{{4\left( {y - 1} \right)}}{{x - 1}}} = 8\end{array}\) Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 1\\y - 1 = 1\\\dfrac{{x - 1}}{{y - 1}} = \dfrac{{y - 1}}{{x - 1}}\end{array} \right. \Leftrightarrow x = y = 2\). Vậy \(\min P = 8 \Leftrightarrow x = y = 2\).
|