Đề thi vào 10 môn Toán Hà Nội năm 2021

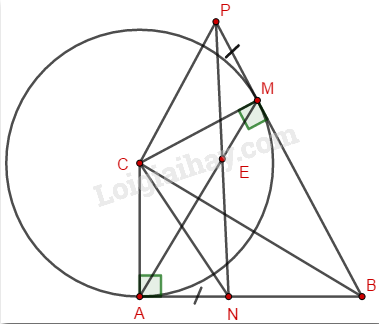
Đề bài

Bài I (2 điểm):

Cho hai biểu thức $A = \dfrac{{\sqrt x }}{{\sqrt x  + 3}}$ và $B = \dfrac{{2\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 9}}{{x - 9}}$ với $x \ge 0,\,\,x \ne 9$.

1) Tính giá trị của biểu thức $A$ khi $x = 16$.                    

2) Chứng minh $A + B = \dfrac{3}{{\sqrt x  + 3}}$. 

Bài II (2,5 điểm):

1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Một tổ sản xuất phải làm xong 4800 bộ đồ bảo hộ y tế trong một số ngày quy định. Thực tế, mỗi ngày tổ đã làm được nhiều hơn 100 bộ đồ bảo hộ y tế so với bộ đồ bảo hộ y tế phải làm trong một ngày theo kế hoạch. Vì thế 8 ngày trước khi hết thời hạn, tổ sản xuất đã làm xong 4800 bộ đồ bảo hộ y tế đó. Hỏi theo kế hoạch, mỗi ngày tổ sản xuất phải làm bao nhiêu bộ đồ bảo hộ y tế? (Giả định rằng số bộ đồ bảo hộ y tế mà tổ đó làm xong trong mỗi ngày là bằng nhau).

2) Một thùng nước có dạng hình trụ với chiều cao 1,6m và bán kính đáy 0,5m. Người ta sơn toàn bộ phía ngoài mặt xung quanh mặt xung quanh của thùng nước này (trừ hai mặt đáy). Tính diện tích bề mặt được sơn của thùng nước (lấy $\pi  \approx 3,14$).

Bài III (2,0 điểm)

1) Giải hệ phương trình $\left\{ {\begin{array}{*{20}{c}}{\dfrac{3}{{x + 1}} - 2y =  - 1}\\{\dfrac{5}{{x + 1}} + 3y = 11}\end{array}} \right.$

2) Trong mặt phẳng tọa độ $Oxy$, cho Parabol $\left( P \right):y = {x^2}$ và đường thẳng $\left( d \right):y = 2x + m - 2$. Tìm tất cả các giá trị của $m$ để $\left( d \right)$ cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1},\,{x_2}$ sao cho $\left| {{x_1} - {x_2}} \right| = 2$.

Bài IV (3,5 điểm)

Cho tam giác $ABC$ vuông tại $A$. Vẽ đường tròn tâm $C$, bán kính $CA$. Từ điểm $B$ kẻ tiếp tuyến $BM$ với đường tròn $\left( {C;CA} \right)$ ($M$ là tiếp điểm, $M$ và $A$nằm khác phía nhau đối với đường thẳng $BC$).

1) Chứng minh bốn điểm $A,C,M$ và $B$ cùng thuộc một đường tròn.

2) Lấy điểm $N$ thuộc đoạn thẳng $AB$( $N$ khác $A$, $N$ khác $B$). Lấy điểm $P$ thuộc tia đối của $MB$ sao cho $MP = AN$. Chứng minh tam giác $CPN$ là tam giác cân và đường thẳng $AM$ đi qua trung điểm của đoạn thẳng $NP$

Bài V (0,5 điểm)

Với các số thực $a$ và $b$ thỏa mãn ${a^2} + {b^2} = 2$, tìm giá trị nhỏ nhất của biểu thức $P = 3\left( {a + b} \right) + ab$.

Lời giải chi tiết

Phương pháp:

1) Thay giá trị $x = 16\,\,\left( {tmdk} \right)$ vào biểu thức $A$ rồi tính giá trị của biểu thức.

2) Quy đồng, biến đổi và rút gọn biểu thức $A + B.$

Từ đó chứng minh được giá trị của $A + B = \dfrac{3}{{\sqrt x  + 3}}$

Cách giải:

1) Điều kiện: $x \ge 0,\,\,x \ne 9.$

Thay $x = 16$ (thỏa mãn điều kiện) vào biểu thức $A$ ta có: 

$A = \dfrac{{\sqrt x }}{{\sqrt x  + 3}} = \dfrac{{\sqrt {16} }}{{\sqrt {16}  + 3}} = \dfrac{4}{{4 + 3}} = \dfrac{4}{7}$.

Vậy khi $x = 16$ thì $A = \dfrac{4}{7}$.

2) Điều kiện: $x \ge 0,\,\,x \ne 9.$

$\begin{array}{l}A + B = \dfrac{{\sqrt x }}{{\sqrt x  + 3}} + \dfrac{{2\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 9}}{{x - 9}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\sqrt x }}{{\sqrt x  + 3}} + \dfrac{{2\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 9}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x  - 3} \right) + 2\sqrt x \left( {\sqrt x  + 3} \right) - 3x - 9}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{x - 3\sqrt x  + 2x + 6\sqrt x  - 3x - 9}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{3\sqrt x  - 9}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{3\left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{{\sqrt x  + 3}}\,\,\left( {dpcm} \right)\end{array}$

Vậy $A + B = \dfrac{3}{{\sqrt x  + 3}}$ (với $x \ge 0,\,\,x \ne 9$).

Phương pháp:

1) Gọi số bộ đồ bảo hộ y tế tổ sản xuất phải làm trong một ngày theo kế hoạch là $x$ (bộ), $\left( {x \in {\mathbb{N}^*}} \right).$

Biểu diễn các đại lượng chưa biết theo các đại lượng đã biết và ẩn $x$ vừa gọi.

Dựa vào giả thiết bài cho để lập phương trình.

Giải phương trình tìm ẩn $x$ và đối chiếu với điều kiện xác định.

Kết luận.

2) Sử dụng công thức tính diện tích xung quanh của hình trụ có chiều cao $h$ và bán kính $r$: ${S_{xq}} = 2\pi rh.$

Cách giải:

1) Gọi số bộ đồ bảo hộ y tế tổ sản xuất phải làm trong một ngày theo kế hoạch là $x$ (bộ), $\left( {x \in {\mathbb{N}^*}} \right).$

$\Rightarrow$ Thời gian theo kế hoạch tổ sản xuất làm xong $4800$ bộ đồ là: $\dfrac{{4800}}{x}$ (ngày).

Thực tế mỗi ngày, tổ đó làm được số bộ đồ bảo hộ y tế là:$x + 100$ (bộ).

$\Rightarrow$ Thời gian thực tế tổ sản xuất làm xong $4800$ bộ đồ là: $\dfrac{{4800}}{{x + 100}}$ (ngày).

Theo đề bài, tổ sản xuất đã làm xong $4800$ bộ đồ trước $8$ ngày so với kế hoạch nên ta có phương trình:

$\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{{4800}}{x} - \dfrac{{4800}}{{x + 100}} = 8\\ \Leftrightarrow 4800\left( {x + 100} \right) - 4800x = 8x\left( {x + 100} \right)\\ \Leftrightarrow 600\left( {x + 100} \right) - 600x = x\left( {x + 100} \right)\\ \Leftrightarrow 600x + 60000 - 600x = {x^2} + 100x\\ \Leftrightarrow {x^2} + 100x - 60000 = 0\end{array}$

Phương trình có: $\Delta ' = {50^2} + 60000 = 62500 > 0$

$\Rightarrow$ Phương trình có hai nghiệm phân biệt: ${x_1} =  - 50 + \sqrt {62500}  = 200\,\,\left( {tm} \right)$ và ${x_2} =  - 50 + \sqrt {62500}  =  - 300\,\,\,\left( {ktm} \right)$

Vậy theo kế hoạch, mỗi ngày tổ sản xuất phải làm $200$ bộ đồ bảo hộ y tế.

2) Thùng nước hình trụ có chiều cao $h = 1,6m$ và bán kính đáy $R = 0,5m$.

Diện tích bề mặt được sơn của thùng nước là:

$2\pi Rh = 2.3,14.0,5.1,6 = 5,024\,\,\,\,\left( {{m^2}} \right)$

Vậy diện tích bề mặt được sơn của thùng nước là $5,024\,{m^2}$.

Phương pháp:

1) Đặt $\dfrac{1}{{x + 1}} = t$, hệ phương trình trở thành $\left\{ {\begin{array}{*{20}{c}}{3t - 2y =  - 1}\\{5t + 3y = 11}\end{array}} \right.$, sau đó sử dụng phương pháp cộng đại số để tìm ra $t$ và $y$ sau đó tìm ra nghiệm $\left( {x;y} \right)$ của phương trình ban đầu.

2) Xét phương trình hoành độ giao điểm của $\left( d \right)$ và $\left( P \right)$, tìm điều kiện để phương trình có 2 nghiệm phân biệt, sử dụng ứng dụng của định lí Vi – ét và điều kiện giả thiết của đề bài để tìm được các giá trị của $m$.

Cách giải:

1) ĐKXĐ: $x \ne  - 1$.

Đặt $\dfrac{1}{{x + 1}} = t$, hệ phương trình trở thành $\left\{ {\begin{array}{*{20}{c}}{3t - 2y =  - 1}\\{5t + 3y = 11}\end{array}} \right.$.

Ta có $\left\{ {\begin{array}{*{20}{c}}{3t - 2y =  - 1}\\{5t + 3y = 11}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{9t - 6y =  - 3}\\{10t + 6y = 22}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}19t = 19\\3t - 2y =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 1\\3 - 2y =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 1\\2y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 1\\y = 2\end{array} \right.$.

Với $t = 1 \Rightarrow \dfrac{1}{{x + 1}} = 1 \Leftrightarrow x + 1 = 1 \Leftrightarrow x = 0$.

Vậy hệ phương trình có nghiệm $\left( {x;y} \right) = \left( {0;2} \right)$.

2) Xét phương trình hoành độ giao điểm của $\left( d \right)$ và $\left( P \right)$:

${x^2} = 2x + m - 2 \Leftrightarrow {x^2} - 2x - m + 2 = 0\,\,\left( * \right)$

$\left( d \right)$ cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ ${x_1},\,\,{x_2}$ $\Rightarrow$ Phương trình (*) phải có 2 nghiệm phân biệt ${x_1},\,\,{x_2}$.

$\Leftrightarrow \Delta ' > 0 \Leftrightarrow 1 + m - 2 > 0 \Leftrightarrow m - 1 > 0 \Leftrightarrow m > 1$.

Khi đó theo định lí Vi-ét ta có:$\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} =  - m + 2}\end{array}} \right.$

Theo giả thiết:

 $\begin{array}{l}\,\,\,\,\,\,\,\left| {{x_1} - {x_2}} \right| = 2\\ \Leftrightarrow {\left| {{x_1} - {x_2}} \right|^2} = 4\\ \Leftrightarrow {x_1}^2 - 2{x_1}{x_2} + {x_2}^2 = 4\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 4\\ \Leftrightarrow 4 - 4\left( { - m + 2} \right) = 4\\ \Leftrightarrow 4\left( { - m + 2} \right) = 0\\ \Leftrightarrow  - m + 2 = 0\\ \Leftrightarrow m = 2\,\,\,\left( {tm} \right)\end{array}$

Vậy $m = 2$.

Phương pháp:

1) Chứng minh tứ giác $ACMB$ nội tiếp một đường tròn suy ra bốn điểm $A,C,M$ và $B$ cùng thuộc một đường tròn

2) Chứng minh $CN = CP$(2 cạnh tương ứng bằng nhau).$\Rightarrow \Delta CNP$ cân tại $C$. (đpcm).

Chứng minh $CE$ là đường cao, đồng thời là đường trung tuyến của $\Delta CNP$$\Rightarrow E$ là trung điểm của $PN$

Cách giải:

1) Ta có: tam giác $ABC$ vuông tại $A$ nên $\angle BAC = {90^0}$

$MB$ là tiếp tuyến của đường tròn $\left( {C;CA} \right)$ nên $\angle CMB = {90^0}$ (định nghĩa tiếp tuyến của đường tròn)

Xét tứ giác $ACMB$ ta có: $\angle CAB + \angle CMB = {90^0} + {90^0} = {180^0}$

$\Rightarrow ACMB$ là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng ${180^0}$).

Hay bốn điểm $A,C,M$ và $B$ cùng thuộc một đường trònbốn điểm $A,C,M$ và $B$ cùng thuộc một đường tròn. (đpcm).

2) Xét tam giác $CAN$ và tam giác $CMP$ có:

$AN = MP\,\,\,\,\left( {gt} \right)$

$\angle CAN = \angle CMP = {90^0}$

$AC = CM$($A,M$ cùng thuộc đường tròn $\left( {C;\,\,CA} \right)$)

$\Rightarrow \Delta CAN = \Delta CMP\,\,\,\left( {c - g - c} \right)$

$\Rightarrow CN = CP$(2 cạnh tương ứng bằng nhau).

$\Rightarrow \Delta CNP$ cân tại $C$. (đpcm).

Gọi $E$ là giao điểm của $AM$ và $PN$.

Vì $\Delta CAN = \Delta CMP\,\,\,\left( {cmt} \right)$ nên:

$\angle ACN = \angle MCP$(2 góc tương ứng bằng nhau)

$\Rightarrow \angle ACM = \angle ACN + \angle NCM$ $= \angle PCM + \angle MCN = \angle NCP$

$\Rightarrow$$\Delta ACM$ và $\Delta CNP$ là hai tam giác cân đỉnh $C$ có $\angle ACM = \angle PCN$

$\Rightarrow \angle CNP = \angle CAM$ (các góc ở đáy của các tam giác cân có góc ở đỉnh bằng nhau)

Hay $\angle CAE = \angle CNE$

$\Rightarrow CANE$ là tứ giác nội tiếp. (tứ giác có hai đỉnh kề 1 cạnh cùng nhìn cạnh đối diện dưới các góc bằng nhau).

$\Rightarrow \angle CEN = {90^0} \Rightarrow CE \bot PN$

Mà $\Delta CNP$ cân tại $C$ (cmt)

$\Rightarrow CE$ là đường cao, đồng thời là đường trung tuyến của $\Delta CNP$

$\Rightarrow E$ là trung điểm của $PN$

Vậy đường thẳng $AM$ đi qua trung điểm của đoạn thẳng $NP$(đpcm).

Phương pháp:

Kết hợp với giả thiết ${a^2} + {b^2} = 2$ biến đổi biểu thức $P = 3\left( {a + b} \right) + ab$ trở thành  $P = \dfrac{1}{2}{\left( {a + b + 3} \right)^2} - \dfrac{{11}}{2}$

Sau đó áp dụng Áp dụng BĐT Bunhiacopxki để tìm giá trị nhỏ nhất của biểu thức ban đầu

Cách giải:

Ta có ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab = 2 + 2ab$ $\Rightarrow ab = \dfrac{{{{\left( {a + b} \right)}^2} - 2}}{2} = \dfrac{1}{2}{\left( {a + b} \right)^2} - 1$.

Khi đó ta có: $P = 3\left( {a + b} \right) + ab = 3\left( {a + b} \right) + \dfrac{1}{2}{\left( {a + b} \right)^2} - 1$.

$\begin{array}{l}P = \dfrac{1}{2}\left[ {{{\left( {a + b} \right)}^2} + 6\left( {a + b} \right) + 9} \right] - \dfrac{{11}}{2}\\P = \dfrac{1}{2}{\left( {a + b + 3} \right)^2} - \dfrac{{11}}{2}\end{array}$

Áp dụng BĐT Bunhiacopxki ta có: ${\left( {a + b} \right)^2} \le 2\left( {{a^2} + {b^2}} \right) = 2.2 = 4$ $\Rightarrow  - 2 \le a + b \le 2$.

$\begin{array}{l} \Rightarrow 1 \le a + b + 3 \le 5\\ \Rightarrow  - 5 \le \dfrac{1}{2}{\left( {a + b + 3} \right)^2} - \dfrac{{11}}{2} \le 7\end{array}$

$\Leftrightarrow {P_{\min }} =  - 5$.

Dấu “=” xảy ra khi và chỉ khi $\left\{ \begin{array}{l}{a^2} + {b^2} = 2\\a = b\\a + b =  - 2\end{array} \right. \Leftrightarrow a = b =  - 1$.

Vậy giá trị nhỏ nhất của biểu thức $P$ bằng $- 5$, đạt được khi $a = b =  - 1$.