Đề thi vào 10 môn Toán Hải Dương năm 2018

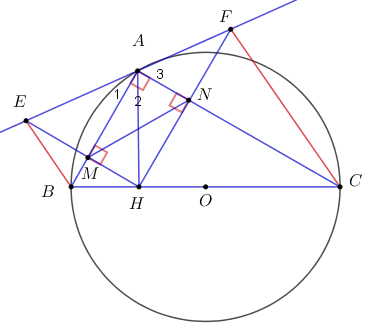
Đề bài

Câu 1 (2 điểm):

Giải phương trình và hệ phương trình:

$1)\;\;\dfrac{{3x + 1}}{2} - x = 1$                                                   $2)\;\;\left\{ \begin{array}{l}3x = 17 - y\\x - 2y = 1\end{array} \right.$

Câu 2 (2 điểm):

1) Tìm $m$ để phương trình ${d_1}:\;y = \left( {{m^2} + 1} \right)x + 2m - 3$ cắt đường thẳng $d:\;y = x - 3$ tại điểm $A$ có hoành độ bằng $- 1.$

2) Rút gọn biểu thức $A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{x + 2\sqrt x  + 1}} + 1$ với $x > 0,\;\;x \ne 1.$

Câu 3 (2 điểm):

1) Quãng đường Hải Dương – Hạ Long dài 100km. Một ô tô đi từ Hải Dương đến Hạ Long rồi nghỉ ở đó 8 giờ 20 phút, sau đó trở về Hải Dương hết tất cả 12 giờ. Tính vận tốc của ô tô lúc đi, biết vận tốc ô tô lúc về nhanh hơn vận  tốc ô tô lúc đi 10 km/h.

2) Tìm $m$ để phương trình ${x^2} - 2mx + {m^2} - 2 = 0$ (x là ẩn, m là tham số) có hai nghiệm phân biệt ${x_1},\;{x_2}$ thỏa mãn $\left| {x_1^3 - x_2^3} \right| = 10\sqrt 2 .$

Câu 4 (3 điểm):

Cho tam giác ABC nội tiếp đường tròn tâm O đường kính BC. Kẻ AH vuông góc với BC (H thuộc BC), gọi M, N lần lượt là hình chiếu vuông góc của H trên AB và AC.

1) Chứng minh $A{C^2} = CH.CB.$

2) Chứng minh tứ giác $BCNM$ nội tiếp và $AC.BM + AB.CN = AH.BC.$

3) Đường thẳng đi qua A cắt tia HM tại E và cắt tia đối của tia NH tại F. Chứng minh BE // CF.

Câu 5 (1 điểm):

Cho phương trình $a{x^2} + bx + c = 0\;\;\left( {a \ne 0} \right)$ có hai nghiệm ${x_1},\;{x_2}$ thỏa mãn $0 \le {x_1} \le {x_2} \le 2.$ Tìm giá trị nhỏ nhất của biểu thức $L = \dfrac{{3{a^2} - ab + ac}}{{5{a^2} - 3ab + {b^2}}}.$

Lời giải chi tiết

Câu 1:

Phương pháp:

1) Quy đồng mẫu phân thức sau đó chuyển vế, đổi dấu để tìm nghiệm của phương trình.

2) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.

Cách giải:

Câu 2:

Phương pháp:

1) Hai đường thẳng cắt nhau tại điểm $A$ có hoành độ bằng $- 1$ thì $- 1$ là nghiệm của phương trình hoành độ giao điểm của hai đồ thị. Từ đó ta tìm được $m.$

2) Quy đồng mẫu các phân thức sau đó biến đổi và rút gọn biểu thức.

Cách giải:

1) Tìm $m$ để phương trình ${d_1}:\;y = \left( {{m^2} + 1} \right)x + 2m - 3$ cắt đường thẳng $d:\;y = x - 3$ tại điểm $A$ có hoành độ bằng $- 1.$

Phương trình hoành độ giao điểm của hai đường thẳng đã cho là:

$\left( {{m^2} + 1} \right)x + 2m - 3 = x - 3 \Leftrightarrow {m^2}x + 2m = 0.\;\;\;\;\left( * \right)$

Hai đường thẳng cắt nhau tại điểm $A$ có hoành độ bằng $- 1$ thì $x =  - 1$ là nghiệm của phương trình (*). Khi đó:

$\begin{array}{l}\left( * \right) \Leftrightarrow  - {m^2} + 2m = 0 \Leftrightarrow m\left( {m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 2\end{array} \right..\end{array}$

Vậy $m = 0$ hoặc $m = 2.$

2) Rút gọn biểu thức $A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{x + 2\sqrt x  + 1}} + 1$ với $x > 0,\;\;x \ne 1.$

Điều kiện: $x > 0,\;\;x \ne 1.$

$\begin{array}{l}A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{x + 2\sqrt x  + 1}} + 1\\\;\;\; = \left( {\dfrac{1}{{\sqrt x \left( {\sqrt x  + 1} \right)}} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{{{\left( {\sqrt x  + 1} \right)}^2}}} + 1\\\;\;\; = \dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x  + 1} \right)}}.\dfrac{{{{\left( {\sqrt x  + 1} \right)}^2}}}{{\sqrt x  - 1}} + 1\\\;\;\; =  - \dfrac{{\sqrt x  + 1}}{{\sqrt x }} + 1\\\;\;\; = \dfrac{{ - \sqrt x  - 1 + \sqrt x }}{{\sqrt x }} =  - \dfrac{1}{{\sqrt x }}.\end{array}$

Câu 3:

Phương pháp:

1) Giải bài toán bằng cách lập phương trình:

+) Gọi ẩn và đặt điều kiện cho ẩn.

+) Biểu diễn các đại lượng chữa biết theo ẩn và đại lượng đã biết.

+) Dựa vào giả thiết của bài toán để lập phương trình.

+) Giải phương trình tìm ẩn và đối chiếu với điều kiện của ẩn rồi kết luận.

2) Phương trình có hai nghiệm phân biệt $\Leftrightarrow \Delta ' > 0.$

+) Áp dụng hệ thức Vi-ét $\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.$ và hệ thức bài cho để tìm giá trị của $m.$

Cách giải:

1) Quãng đường Hải Dương – Hạ Long dài 100km. Một ô tô đi từ Hải Dương đến Hạ Long rồi nghỉ ở đó 8 giờ 20 phút, sau đó trở về Hải Dương hết tất cả 12 giờ. Tính vận tốc của ô tô lúc đi, biết vận tốc ô tô lúc về nhanh hơn vận  tốc ô tô lúc đi 10 km/h.

Gọi vận tốc của ô tô lúc đi là $x\;\left( {km/h} \right),\;\;\left( {x > 0} \right).$

Khi đó vận tốc lúc về của ô tô là: $x + 10\;\;\left( {km/h} \right).$

Thời gian ô tô đi từ Hải Dương đến Hạ Long là: $\dfrac{{100}}{x}\;\;\left( h \right).$

Thời gian ô tô đi từ Hạ Long về Hải Dương là: $\dfrac{{100}}{{x + 10}}\;\;\left( h \right).$

Đổi $8$ giờ $20$ phút $= \dfrac{{25}}{3}$ giờ.

Theo đề bài ta có phương trình:

$\begin{array}{l}\;\;\;\;\dfrac{{100}}{x} + \dfrac{{25}}{3} + \dfrac{{100}}{{x + 10}} = 12\\ \Leftrightarrow \dfrac{{100}}{x} + \dfrac{{100}}{{x + 10}} - \dfrac{{11}}{3} = 0\\ \Leftrightarrow 300\left( {x + 10} \right) + 300x - 11x\left( {x + 10} \right) = 0\\ \Leftrightarrow 600x + 3000 - 11{x^2} - 110x = 0\\ \Leftrightarrow 11{x^2} - 490x - 3000 = 0\\ \Leftrightarrow \left( {x - 50} \right)\left( {11x + 60} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 50 = 0\\11x + 60 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 50\;\;\left( {tm} \right)\\x =  - \dfrac{{60}}{{11}}\;\;\left( {ktm} \right)\end{array} \right..\end{array}$

Vậy vận tốc của ô tô lúc đi là $50\;km/h.$

2) Tìm $m$ để phương trình ${x^2} - 2mx + {m^2} - 2 = 0$ (x là ẩn, m là tham số) có hai nghiệm phân biệt ${x_1},\;{x_2}$ thỏa mãn $\left| {x_1^3 - x_2^3} \right| = 10\sqrt 2 .$

Phương trình có hai nghiệm phân biệt $\Leftrightarrow \Delta ' > 0 \Leftrightarrow {m^2} - {m^2} + 2 > 0\; \Leftrightarrow 2 > 0\;\forall m$

$\Rightarrow$ Phương trình luôn có hai nghiệm ${x_1},\;\;{x_2}$ với mọi $m.$

Áp dụng hệ thức Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = {m^2} - 2\end{array} \right..$

Theo đề bài ta có: $\left| {x_1^3 - x_2^3} \right| = 10\sqrt 2$

$\begin{array}{l} \Leftrightarrow \left| {\left( {{x_1} - {x_2}} \right)\left( {x_1^2 + {x_1}{x_2} + x_2^2} \right)} \right| = 10\sqrt 2 \\ \Leftrightarrow \left| {\left( {{x_1} - {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right]} \right| = 10\sqrt 2 \\ \Leftrightarrow {\left| {\left( {{x_1} - {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right]} \right|^2} = 200\\ \Leftrightarrow {\left( {{x_1} - {x_2}} \right)^2}{\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right]^2} = 200\\ \Leftrightarrow \left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right]{\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right]^2} = 200\\ \Leftrightarrow \left[ {4{m^2} - 4\left( {{m^2} - 2} \right)} \right]{\left[ {4{m^2} - {m^2} + 2} \right]^2} = 200\\ \Leftrightarrow 8{\left( {3{m^2} + 2} \right)^2} = 200\\ \Leftrightarrow {\left( {3{m^2} + 2} \right)^2} = 25\\ \Leftrightarrow 3{m^2} + 2 = 5\;\;\;\left( {do\;\;3{m^2} + 2 > 0\;\;\forall m} \right)\\ \Leftrightarrow {m^2} = 1\\ \Leftrightarrow m =  \pm 1.\end{array}$

Vậy $m =  \pm 1$ thỏa mãn bài toán.

Câu 4:

Phương pháp:

a) Áp dụng hệ thức lượng trong tam giác vuông.

b) Chứng minh tam giác đồng dạng.

c)

Cách giải:

Cho tam giác ABC nội tiếp đường tròn tâm O đường kính BC. Kẻ AH vuông góc với BC (H thuộc BC), gọi M, N lần lượt là hình chiếu vuông góc của H trên AB và AC.

1) Chứng minh $A{C^2} = CH.CB.$

Xét đường tròn ngoại tiếp tam giác ABC có đường kính BC ta có:

$\widehat {BAC}$ là góc nội tiếp chắn nửa đường tròn $\Rightarrow \widehat {BAC} = {90^0} \Rightarrow$ $\Delta ABC$ vuông tại $A.$

Xét tam giác $ABC$ có đường cao ta có:

$A{C^2} = CH.CB$ (hệ thức lượng trong tam giác vuông). (đpcm)

2) Chứng minh tứ giác $BCNM$ nội tiếp và $AC.BM + AB.CN = AH.BC.$

+) Ta có $ANHM$ là hình chữ nhật do có 3 góc vuông.

$\Rightarrow AN//MH,\;\;AM//HN.$

$\Rightarrow \widehat {MAH} = \widehat {AMN}$ (tính chất).

Lại có $\widehat {ABH} = {90^0} - \widehat {BAH}\\\widehat {ANM} = {90^0} - \widehat {AMN}\\  \Rightarrow \widehat {ABH} = \widehat {ANM}\;\;hay\;\;\widehat {MBC} = \widehat {ANM}$ 

Xét tứ giác $BCNM$ ta có: $\widehat {MBC} = \widehat {ANM}\;\;\left( {cmt} \right)$

$\Rightarrow BMNC$ là tứ giác nội tiếp (góc trong tại một đỉnh bằng góc ngoài tại đỉnh đối diện).

+) Xét $\Delta BMH$ và $\Delta AHC$ ta có:

$\widehat {MBH} = \widehat {HAC}\;\;$(cùng phụ với $\widehat {ACH}$)

$\begin{array}{l}\widehat {BMH} = \widehat {AHC} = {90^0}\\ \Rightarrow \Delta BMH \sim \Delta AHC\;\;\left( {g - g} \right)\\ \Rightarrow \dfrac{{BM}}{{AH}} = \dfrac{{BH}}{{AC}} \Leftrightarrow AC.BM = AH.BH.\end{array}$

Xét $\Delta CNH$ và $\Delta BAH$ ta có:

$\widehat {NCH} = \widehat {BAH}$ (cùng phụ với $\widehat {ABH}$)

$\begin{array}{l}\widehat {CNH} = \widehat {AHB} = {90^0}\\ \Rightarrow \Delta CNH \sim \Delta AHB\left( {g - g} \right)\\ \Rightarrow \dfrac{{CN}}{{AH}} = \dfrac{{CH}}{{AB}} \Rightarrow AB.CN = AH.CH.\\ \Rightarrow AC.BM + AB.CN = AH.BH + AH.CH = AH\left( {BH.CH} \right) = AH.BC\;\;\left( {dpcm} \right)\end{array}$

3) Đường thẳng đi qua A cắt tia HM tại E và cắt tia đối của tia NH tại F. Chứng minh BE // CF.

Ta có :  

$\Rightarrow \dfrac{{AN}}{{ME}} = \dfrac{{NF}}{{AM}} \Rightarrow AN.AM = NF.ME\,\,\left( 1 \right)$

Lại có :

Mặt khác $AM.AN = MH.NH\,\,\left( {AM = NH;AN = MH} \right)\,\,\,\left( 3 \right)$

Từ (1) , (2), (3)  suy ra $NF.ME = BM.NC \Rightarrow \dfrac{{NF}}{{NC}} = \dfrac{{BM}}{{ME}} \Rightarrow \dfrac{{ME}}{{NC}} = \dfrac{{BM}}{{NF}}$

Mà $\widehat {BME} = \widehat {CNF} = {90^0}$

Suy ra $\Delta BME \sim \Delta FNC\left( {c - g - c} \right) \Rightarrow \widehat {CFN} = \widehat {EBM}$

Ta lại có $\widehat {NFA} = \widehat {MEA}\left( {Do\,\,AB\parallel HF} \right)$

Nên ta có : $\begin{array}{l}\widehat {CFE} + \widehat {BEF} = \widehat {CFN} + \widehat {NFA} + \widehat {BEF} = \widehat {EBM} + \widehat {MAE} + \widehat {BEF}\\ \Rightarrow \widehat {CFE} + \widehat {BEF} = \widehat {EBA} + \widehat {BAE} + \widehat {BEF} = {180^0}\end{array}$

(Theo định lý tổng ba góc trong tam giác EBA).

Vậy BE//CF

Câu 5:

Cách giải:

Phương trình có hai nghiệm ${x_1},\;{x_2}$ thỏa mãn $0 \le {x_1} \le {x_2} \le 2$

$\Leftrightarrow \left\{ \begin{array}{l}\Delta  \ge 0\\af\left( 0 \right) \ge 0\\af\left( 2 \right) \ge 0\\\dfrac{S}{2} > 0\\\dfrac{S}{2} < 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b^2} - 4ac > 0\\ac \ge 0\\a\left( {4a + 2b + c} \right) \ge 0\\ - \dfrac{b}{{2a}} > 0\\ - \dfrac{b}{{2a}} < 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b^2} \ge 4ac\\ac \ge 0\\a\left( {4a + 2b + c} \right) \ge 0\\\dfrac{b}{{2a}} < 0\\\dfrac{{4a + b}}{{2a}} > 0\end{array} \right..$

Theo hệ thức Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right..$

Theo đề bài ta có:

$\begin{array}{l}L = \dfrac{{3{a^2} - ab + ac}}{{5{a^2} - 3ab + {b^2}}} = \dfrac{{3 - \dfrac{b}{a} + \dfrac{c}{a}}}{{5 - 3.\dfrac{b}{a} + {{\left( {\dfrac{b}{a}} \right)}^2}}}\;\;\left( {do\;\;a \ne 0} \right)\\\;\; = \dfrac{{3 + \left( {{x_1} + {x_2}} \right) + {x_1}{x_2}}}{{5 + 3\left( {{x_1} + {x_2}} \right) + {{\left( {{x_1} + {x_2}} \right)}^2}}}\;\;\;\left( {L > 0\;\;\forall \;0 \le {x_1} \le {x_2} \le 2} \right)\\\;\; = \dfrac{{3 + {x_1} + {x_2} + {x_1}{x_2}}}{{5 + 3{x_1} + 3{x_2} + x_1^2 + x_2^2 + 2{x_1}{x_2}}}.\\ \Rightarrow \dfrac{1}{L} = \dfrac{{5 + 3{x_1} + 3{x_2} + x_1^2 + x_2^2 + 2{x_1}{x_2}}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}.\end{array}$

Vì $0 \le {x_1} \le {x_2} \le 2 \Rightarrow \left\{ \begin{array}{l}x_1^2 \le 2{x_1}\\x_2^2 \le 2{x_2}\\{x_1} - 2 \le 0\\{x_2} - 2 \le 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x_1^2 + x_2^2 \le 2{x_1} + 2{x_2}\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) \ge 0\end{array} \right..$

$\begin{array}{l} \Rightarrow \dfrac{1}{L} \le \dfrac{{5 + 3{x_1} + 3{x_2} + 2{x_1} + 2{x_2} + 2{x_1}{x_2}}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}} = \dfrac{{5 + 5{x_1} + 5{x_2} + 2{x_1}{x_2}}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}\\\;\;\;\;\;\;\; = \dfrac{{3{x_1}{x_2} + 3{x_1} + 3{x_2} + 9 - {x_1}{x_2} + 2{x_1} + 2{x_2} - 4}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}\\\;\;\;\;\;\;\; = \dfrac{{3\left( {3 + {x_1} + {x_2} + {x_1}{x_2}} \right) - \left( {{x_2} - 2} \right){x_1} + 2\left( {{x_2} - 2} \right)}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}\\\;\;\;\;\;\;\; = 3 - \dfrac{{\left( {{x_2} - 2} \right)\left( {{x_1} - 2} \right)}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}} \le 3\;\;\;\left( {do\;\;\left( {{x_2} - 2} \right)\left( {{x_1} - 2} \right) \ge 0} \right)\\ \Rightarrow 0 \le \dfrac{1}{L} \le 3 \Leftrightarrow 3L \ge 1 \Leftrightarrow L \ge \dfrac{1}{3}\\ \Rightarrow Min\;L = \dfrac{1}{3}.\end{array}$

Dấu “=” xảy ra $\Leftrightarrow \left\{ \begin{array}{l}x_1^2 = 2{x_1}\\x_2^2 = 2{x_2}\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1}\left( {{x_1} - 2} \right) = 0\\{x_2}\left( {{x_2} - 2} \right) = 0\\\left[ \begin{array}{l}{x_1} - 2 = 0\\{x_2} - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x_1} = 2\\{x_2} = 2\end{array} \right.\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}{x_1} = 0\\{x_1} = 2\end{array} \right.\\\left[ \begin{array}{l}{x_2} = 0\\{x_2} = 2\end{array} \right.\\\left[ \begin{array}{l}{x_1} = 2\\{x_2} = 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{x_1} = 0\\{x_2} = 2\end{array} \right.\\\left\{ \begin{array}{l}{x_1} = 2\\{x_2} = 0\end{array} \right.\\\left\{ \begin{array}{l}{x_1} = 2\\{x_2} = 2\end{array} \right.\end{array} \right..$

Vậy $Min\;L = \dfrac{1}{3}\;\;khi\;\;\left( {{x_1};\;{x_2}} \right) = \left\{ {\left( {0;\;2} \right),\;\left( {2;\;0} \right),\;\left( {2;\;2} \right)} \right\}.$