Đề thi vào 10 môn Toán Khánh Hòa năm 2020

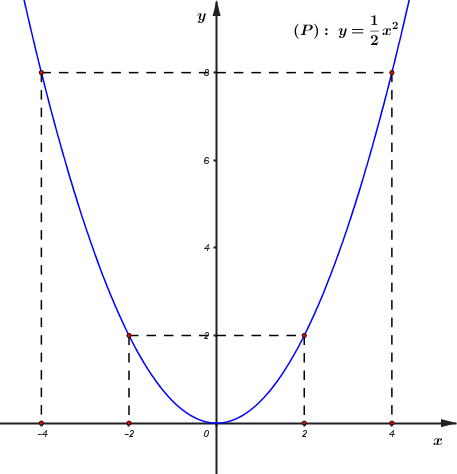
Đề bài

Câu 1: 

a) Rút gọn biểu thức $A = \left( {3\sqrt 2  - \sqrt 8 } \right)\sqrt 2$.

b) Giải phương trình ${x^2} - 5x + 4 = 0$

Câu 2:   Trên mặt phẳng $Oxy,$ cho parabol $\left( P \right):\,\,\,y = \dfrac{1}{2}{x^2}$ và đường thẳng $\left( d \right):\,\,\,y = x - m$ ($m$ là tham số).

a) Vẽ parabol $\left( P \right):\,\,\,y = \dfrac{1}{2}{x^2}.$

b) Với $m = 0,$ tìm tọa độ giao điểm của $\left( d \right)$ và $\left( P \right)$ bằng phương pháp đại số.

c) Tìm điều kiện của $m$ để $\left( d \right)$ và $\left( P \right)$ tại hai điểm phân biệt.

Câu 3:    Để chung tay phòng chống dịch COVID-19, hai trường A và B trên địa bàn tỉnh Khánh Hòa phát động phong trào quyên góp ủng hộ người dân có hoàn cảnh khó khăn. Hai trường đã quyên góp được 1137 phần quà gồm mì tôm (đơn vị thùng) và gạo (đơn vị bao). Trong đó, mỗi lớp của trường A ủng hộ được 8 thùng mì và 5 bao gạo, mỗi lớp của trường B ủng hộ được 7 thùng mì và 8 bao gạo. Biết số bao gạo ít hơn số thùng mì là 75 phần quà. Hỏi mỗi trường có bao nhiêu lớp?

Câu 4: 

Cho đường tròn $\left( O \right)$ và một điểm $I$ nằm ngoài đường tròn. Qua $I$ kẻ hai tiếp tuyến $IM$ và $IN$ với đường tròn $\left( O \right).$ Gọi $K$ là điểm đối xứng với $M$ qua $O.$ Đường thẳng $IK$ cắt đường tròn $\left( O \right)$ tại $H.$

a) Chứng minh tứ giác $IMON$ nội tiếp đường tròn.

b) Chứng minh $IM.IN = IH.IK.$

c) Kẻ $NP \bot MK.$ Chứng minh đường thẳng $IK$ đi qua trung điểm của $NP.$

Câu 5: 

Cho $x,\,\,y$ là các số thực thỏa: $x,\,\,y > 0$ và $x + y \ge \dfrac{7}{2}$.

Tìm giá trị nhỏ nhất của biểu thức $P = \dfrac{{13x}}{3} + \dfrac{{10y}}{3} + \dfrac{1}{{2x}} + \dfrac{9}{y}$ 

Lời giải chi tiết

Câu 1 (2,00 điểm) (Không sử dụng máy tính cầm tay)

Cách giải:

a) Rút gọn biểu thức $A = \left( {3\sqrt 2  - \sqrt 8 } \right)\sqrt 2$.

Ta có:

$\begin{array}{l}A = \left( {3\sqrt 2  - \sqrt 8 } \right)\sqrt 2 \\A = \left( {3\sqrt 2  - \sqrt {{2^2}.2} } \right)\sqrt 2 \\A = \left( {3\sqrt 2  - 2\sqrt 2 } \right)\sqrt 2 \\A = \sqrt 2 .\sqrt 2 \\A = 2\end{array}$

Vậy $A = 2$.

b) Giải phương trình ${x^2} - 5x + 4 = 0$

$\begin{array}{l}\,\,\,\,\,\,{x^2} - 5x + 4 = 0\\ \Leftrightarrow {x^2} - 4x - x + 4 = 0\\ \Leftrightarrow \left( {{x^2} - 4x} \right) - \left( {x - 4} \right) = 0\\ \Leftrightarrow x\left( {x - 4} \right) - \left( {x - 4} \right) = 0\\ \Leftrightarrow \left( {x - 4} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 4 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 1\end{array} \right.\end{array}$

Vậy tập nghiệm của phương trình là $S = \left\{ {1;4} \right\}$.

Câu 2 (2,5 điểm)

Cách giải:

Trên mặt phẳng $Oxy,$ cho parabol $\left( P \right):\,\,\,y = \dfrac{1}{2}{x^2}$ và đường thẳng $\left( d \right):\,\,\,y = x - m$ ($m$ là tham số).

a) Vẽ parabol $\left( P \right):\,\,\,y = \dfrac{1}{2}{x^2}.$

Ta có bảng giá trị:

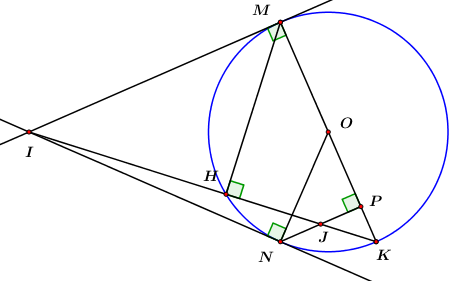
Do đó, $\left( P \right):\,\,y = \dfrac{1}{2}{x^2}$ là đường cong đi qua các điểm: $\left( { - 4;\,\,8} \right),\,\,\left( { - 2;\,\,2} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {2;\,\,2} \right),\,\,\left( {4;\,\,8} \right).$

b) Với $m = 0,$ tìm tọa độ giao điểm của $\left( d \right)$ và $\left( P \right)$ bằng phương pháp đại số.

Với $m = 0$ ta có: $\left( d \right):\,\,\,y = x.$

Phương trình hoành độ giao điểm của đường thẳng $\left( d \right)$ và đồ thị hàm số $\left( P \right)$ là:

$\begin{array}{l}\,\,\,\,\,\dfrac{1}{2}{x^2} = x \Leftrightarrow \dfrac{1}{2}{x^2} - x = 0\\ \Leftrightarrow {x^2} - 2x = 0\\ \Leftrightarrow x\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\end{array}$

+) Với $x = 0 \Rightarrow y = 0$

+) Với $x = 2 \Rightarrow y = 2$

Vậy với $m = 0$ thì đường thẳng $\left( d \right)$ cắt parabol $\left( P \right)$ tại hai điểm phân biệt có tọa độ là $\left( {0;\,\,0} \right)$ và $\left( {2;\,\,2} \right).$

c) Tìm điều kiện của $m$ để $\left( d \right)$ và $\left( P \right)$ tại hai điểm phân biệt.

Phương trình hoành độ giao điểm của đường thẳng $\left( d \right)$ và đồ thị hàm số $\left( P \right)$ là:

$\dfrac{1}{2}{x^2} = x - m \Leftrightarrow {x^2} - 2x + 2m = 0\,\,\,\left( * \right)$

Đường thẳng $\left( d \right)$ cắt parabol $\left( P \right)$ tại hai điểm phân biệt $\Leftrightarrow$ Phương trình (*) có hai nghiệm phân biệt.

$\Leftrightarrow \Delta ' > 0 \Leftrightarrow 1 - 2m > 0 \Leftrightarrow m < \dfrac{1}{2}$.

Vậy với $m < \dfrac{1}{2}$ thì  $\left( d \right)$ cắt $\left( P \right)$ tại hai điểm phân biệt.

Câu 3 (1,50 điểm):

Cách giải:

Để chung tay phòng chống dịch COVID-19, hai trường A và B trên địa bàn tỉnh Khánh Hòa phát động phong trào quyên góp ủng hộ người dân có hoàn cảnh khó khăn. Hai trường đã quyên góp được 1137 phần quà gồm mì tôm (đơn vị thùng) và gạo (đơn vị bao). Trong đó, mỗi lớp của trường A ủng hộ được 8 thùng mì và 5 bao gạo, mỗi lớp của trường B ủng hộ được 7 thùng mì và 8 bao gạo. Biết số bao gạo ít hơn số thùng mì là 75 phần quà. Hỏi mỗi trường có bao nhiêu lớp?

Gọi số lớp ở trường A là $x$ (lớp) (ĐK: $x \in {\mathbb{N}^*}$), số lớp ở trường B là $y$ (lớp) (ĐK: $y \in {\mathbb{N}^*}$).

Số thùng mì trường A ủng hộ là: $8x$ (thùng), số bao gạo trường A ủng hộ là $5x$ (bao).

Số thùng mì trường B ủng hộ là: $7y$ (thùng), số bao gạo trường B ủng hộ là $8y$ (bao).

Vì hai trường đã quyên góp được 1137 phần quà nên ta có phương trình:

$8x + 5x + 7y + 8y = 1137 \Leftrightarrow 13x + 15y = 1137$.

Vì số bao gạo ít hơn số thùng mỳ là 75 phần quà nên ta có phương trình:

$\left( {8x + 7y} \right) - \left( {5x + 8y} \right) = 75 \Leftrightarrow 3x - y = 75$.

Khi đó ta có hệ phương trình:

$\left\{ \begin{array}{l}13x + 15y = 1137\\3x - y = 75\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}13x + 15y = 1137\\45x - 15y = 1125\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}58x = 2262\\3x - y = 75\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 39\\3.39 - y = 75\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}x = 39\\y = 42\end{array} \right.\,\,\left( {tm} \right)$.

Vậy trường A có 39 lớp, trường B có 42 lớp.

Câu 4 (3,00 điểm)

Cách giải:

Cho đường tròn $\left( O \right)$ và một điểm $I$ nằm ngoài đường tròn. Qua $I$ kẻ hai tiếp tuyến $IM$ và $IN$ với đường tròn $\left( O \right).$ Gọi $K$ là điểm đối xứng với $M$ qua $O.$ Đường thẳng $IK$ cắt đường tròn $\left( O \right)$ tại $H.$

a) Chứng minh tứ giác $IMON$ nội tiếp đường tròn.

Ta có: $IM,\,\,IN$ là các tiếp tuyến của $\left( O \right)$ tại $M,\,\,N$ $\Rightarrow \angle IMO = \angle INO = {90^0}$ (định nghĩa).

Xét tứ giác $IMON$ ta có:  $\angle IMO + \angle INO = {90^0} + {90^0} = {180^0}$

Mà hai góc này là hai góc đối diện $\Rightarrow IMON$ là tứ giác nội tiếp đường tròn (dhnb).

b) Chứng minh $IM.IN = IH.IK.$

Ta có: $K$ là điểm đối xứng của $M$ qua $O$ $\Rightarrow O$ là trung điểm của $MK$ và $MK$ là đường kính của $\left( O \right).$

Ta có: $\angle MHK$ là góc nội tiếp chắn nửa đường tròn $\left( O \right).$

$\Rightarrow \angle MHK = {90^0}$ hay $MH \bot HK.$

Áp dụng hệ thức lượng cho $\Delta IMK$ vuông tại $M$ có đường cao $MH$ ta có: $I{M^2} = IH.IK$.

Mà $IM = IN$ (tính chất hai tiếp tuyến cắt nhau).

$\Rightarrow I{M^2} = IN.IM = IH.IK$ (đpcm).

c) Kẻ $NP \bot MK.$ Chứng minh đường thẳng $IK$ đi qua trung điểm của $NP.$

Gọi $IK \cap NP = \left\{ J \right\}$, $IK \cap MN = \left\{ E \right\}$.

Ta có: $IM = IN\,\,\,\left( {cmt} \right)$ nên tam giác $IMN$ cân tại $I$ (tính chất tam giác cân).

$\Rightarrow \angle INM = \angle IMN$ (2 góc ở đáy tam giác cân).

Lại có $\angle MNP = \angle IMN$ (so le trong do $NP\parallel MI$ - cùng vuông góc với $MK$).

$\Rightarrow \angle INM = \angle MNP$ $\left( { = \angle IMN} \right)$.

$\Rightarrow NE$ là phân giác trong $\angle INJ$.

Lại có $\angle MNK$ là góc nội tiếp chắn nửa đường tròn $\left( O \right)$ nên $\angle MNK = {90^0}$, do đó $NK \bot NE$ nên $NK$ là phân giác ngoài của $\angle INJ$.

Áp dụng tính chất đường phân giác ta có: $\dfrac{{NI}}{{NJ}} = \dfrac{{EI}}{{EJ}} = \dfrac{{KI}}{{KJ}}$.

Áp dụng định lí Ta-let do $NP\parallel MI$ ta có: $\dfrac{{EI}}{{EJ}} = \dfrac{{MI}}{{NJ}}$, $\dfrac{{KI}}{{KJ}} = \dfrac{{MI}}{{JP}}$.

Từ đó suy ra $\dfrac{{MI}}{{NJ}} = \dfrac{{MI}}{{JP}} \Rightarrow NJ = JP$ $\Rightarrow J$ là trung điểm của $NP$.

Vậy đường thẳng $IK$ đi qua trung điểm của $NP$ (đpcm).

Câu 5 (1,00 điểm):

Cách giải:

Cho $x,\,\,y$ là các số thực thỏa: $x,\,\,y > 0$ và $x + y \ge \dfrac{7}{2}$.

Tìm giá trị nhỏ nhất của biểu thức $P = \dfrac{{13x}}{3} + \dfrac{{10y}}{3} + \dfrac{1}{{2x}} + \dfrac{9}{y}$.

Ta có:

$\begin{array}{l}P = \dfrac{{13x}}{3} + \dfrac{{10y}}{3} + \dfrac{1}{{2x}} + \dfrac{9}{y}\\P = \left( {2x + \dfrac{1}{{2x}}} \right) + \left( {y + \dfrac{9}{y}} \right) + \dfrac{7}{3}\left( {x + y} \right)\end{array}$

Áp dụng BĐT Cô-si ta có:

$\left\{ \begin{array}{l}2x + \dfrac{1}{{2x}} \ge 2\sqrt {2x.\dfrac{1}{{2x}}}  = 2\\y + \dfrac{9}{y} \ge 2\sqrt {y.\dfrac{9}{y}}  = 6\\x + y \ge \dfrac{7}{2}\,\,\,\left( {gt} \right)\end{array} \right.$

$\Rightarrow P \ge 2 + 6 + \dfrac{7}{3}.\dfrac{7}{2} = \dfrac{{97}}{6}$.

Dấu “=” xảy ra $\Leftrightarrow \left\{ \begin{array}{l}2x = \dfrac{1}{{2x}}\\y = \dfrac{9}{y}\\x + y = \dfrac{7}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{x^2} = 1\\{y^2} = 9\\x + y = \dfrac{7}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = 3\end{array} \right.$.

Vậy ${P_{\min }} = \dfrac{{97}}{6} \Leftrightarrow x = \dfrac{1}{2},\,\,y = 3$.