Đề thi vào 10 môn Toán Nam Định năm 2020Tải vềPhần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
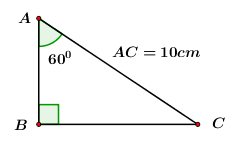
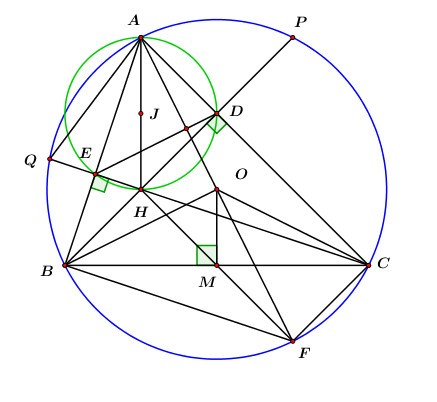
Đề bài Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm. Câu 1. Điều kiện để biểu thức \(2020\sqrt {3 - x} \) có nghĩa là: A. \(x \ge 3\) B. \(x \ne 3\) C. \(x \le 3\) D. \(x < 3\) Câu 2. Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)? A. \(y = - 5x + 3\) B. \(y = 5\) C. \(y = 5x - 1\) D. \(y = - 5\) Câu 3. Hệ phương trình \(\left\{ \begin{array}{l}5x - 2y = 5\\2x + y = 11\end{array} \right.\) có nghiệm \(\left( {x;\,\,y} \right)\) là: A. \(\left( {3;\,\,5} \right)\) B. \(\left( {5;\,\,3} \right)\) C. \(\left( { - 5;\,\,3} \right)\) D. \(\left( {3;\, - 5} \right)\) Câu 4. Tìm \(a,\) biết đồ thị của hàm số \(y = 2x - a\) đi qua điểm \(\left( {0;\,\,1} \right).\) A. \(a = 2\) B. \(a = - 1\) C. \(a = 1\) D. \(a = - 2\) Câu 5. Trong các phương trình sau, phương trình nào có nghiệm kép? A. \({x^2} + 8x + 7 = 0\) B. \({x^2} - 9 = 0\) C. \({x^2} - 7x + 4 = 0\) D. \({x^2} - 6x + 9 = 0\) Câu 6. Cho \(\Delta ABC\) vuông tại \(B\) biết \(AC = 10cm,\) \(\angle A = {60^0}.\) Độ dài đoạn \(AB\) là: A. \(5\sqrt 3 \,cm\) B. \(10\sqrt 3 \,cm\) C. \(5cm\) D. \(\dfrac{{10\sqrt 3 }}{3}\,cm\) Câu 7. Cho đường tròn \(\left( {O;\,\,5cm} \right)\) và đường tròn \(\left( {O';\,\,7cm} \right),\) biết \(OO' = 2cm.\) Vị trí tương đối của hai đường tròn đó là: A. Cắt nhau. B. Tiếp xúc trong. C. Tiếp xúc ngoài. D. Đụng nhau. Câu 8. Diện tích xung quanh hình trụ có bán kính đáy \(5cm,\) chiều cao \(2cm\) là: A. \(20\pi \,c{m^2}\) B. \(10\pi \,c{m^2}\) C. \(20\,c{m^2}\) D. \(10\,c{m^2}\) Phần II. Tự luận (8 điểm): Bài 1. (1,5 điểm) 1) Chứng minh đẳng thức: \(\sqrt {{{\left( {\sqrt 5 - 4} \right)}^2}} - \sqrt 5 + \sqrt {20} = 4.\) 2) Rút gọn biểu thức: \(P = \left( {\dfrac{1}{{\sqrt x + 2}} + \dfrac{1}{{\sqrt x - 2}}} \right):\dfrac{2}{{x - 2\sqrt x }}\) với \(x > 0,\,\,x \ne 4.\) Bài 2. (1,5 điểm) Cho phương trình: \({x^2} - \left( {2m + 1} \right)x + {m^2} + m = 0\) (với \(m\) là tham số). 1) Giải phương trình khi \(m = 4.\) 2) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt \({x_1};\,{x_2}\) với mọi \(m.\) Tìm \(m\) để \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 - 5{x_1}{x_2} = - 17.\) Bài 3. (1,0 điểm) Giải hệ phương trình: \(\left\{ \begin{array}{l}2{\left( {x - 2} \right)^2} + \dfrac{1}{{\sqrt {y + 5} }} = 3\\{\left( {x - 2} \right)^2} - \dfrac{2}{{\sqrt {y + 5} }} = - 1\end{array} \right..\) Bài 4. (3,0 điểm) Cho \(\Delta ABC\) là tam giác nhọn nội tiếp đường tròn \(\left( {O;\,\,R} \right).\) Hai đường cao \(BD,\,\,CE\) của \(\Delta ABC\) cắt nhau tại \(H.\) Các tia \(BD,\,\,CE\) cắt đường tròn \(\left( {O;\,\,R} \right)\) lần lượt tại điểm thứ hai là \(P,\,Q.\) 1) Chứng minh tứ giác \(BCDE\) nội tiếp và \(cung\,\,AP = \,\,cung\,\,AQ.\) 2) Chứng minh \(E\) là trung điểm của \(HQ\) và \(OA \bot DE.\) 3) Cho \(CAB = {60^0},\,\,R = 6cm.\) Tính bán kính đường tròn ngoại tiếp \(\Delta AED.\) Bài 5. (1,0 điểm) 1) Giải phương trình: \(\sqrt 2 \sqrt {2{x^2} + x + 1} - \sqrt {4x - 1} + 2{x^2} + 3x - 3 = 0.\) 2) Cho các số thực dương \(a,\,\,b,\,\,c\) thỏa mãn: \(ab + bc + ca = 3.\) Chứng minh: \(\dfrac{{{a^3}}}{{b + 2c}} + \dfrac{{{b^3}}}{{c + 2a}} + \dfrac{{{c^3}}}{{a + 2b}} \ge 1.\) Lời giải chi tiết Phần I: Trắc nghiệm
Câu 1 - Căn bậc hai Phương pháp: Biểu thức: \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\) Cách giải: Biểu thức: \(2020\sqrt {3 - x} \) xác định \( \Leftrightarrow 3 - x \ge 0\) \( \Leftrightarrow x \le 3.\) Chọn C. Câu 2 - Hàm số bậc nhất Phương pháp: Hàm số bậc nhất \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R}\) \(a > 0.\) Cách giải: Trong các đáp án đã cho, chỉ có hàm số \(y = 5x - 1\) là hàm số bậc nhất có \(a = 5 > 0\) \( \Rightarrow \) Hàm số \(y = 5x - 1\) là hàm số đồng biến trên \(\mathbb{R}.\) Chọn C. Câu 3 - Giải hệ phương trình bằng phương pháp cộng đại số Phương pháp: Giải hệ phương trình đã cho bằng phương pháp cộng đại số. Cách giải: Ta có: \(\left\{ \begin{array}{l}5x - 2y = 5\\2x + y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x - 2y = 5\\4x + 2y = 22\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}9x = 27\\y = 11 - 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 11 - 2.3 = 5\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( {3;\,\,5} \right).\) Chọn A. Câu 4 - Đồ thị của hàm số y = ax + b (a ≠ 0) Phương pháp: Thay tọa độ điểm \(\left( {0;\,\,1} \right)\) vào công thức hàm số \(y = 2x - a\) để tìm \(a.\) Cách giải: Thay tọa độ điểm \(\left( {0;\,\,1} \right)\) vào công thức hàm số \(y = 2x - a\) ta được: \(1 = 2.0 - a \Leftrightarrow a = - 1.\) Chọn B. Câu 5 - Công thức nghiệm của phương trình bậc hai Phương pháp: Phương trình \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) có nghiệm kép \( \Leftrightarrow \Delta = {b^2} - 4ac = 0\) hoặc \(\Delta ' = b{'^2} - ac = 0\,\,\,\left( {b = 2b'} \right).\) Cách giải: +) Xét đáp án A: \({x^2} + 8x + 7 = 0\) ta có: \(\Delta ' = {4^2} - 7 = 9 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt. \( \Rightarrow \) Loại đáp án A. +) Xét đáp án B: \({x^2} - 9 = 0 \Leftrightarrow {x^2} = 9\) \( \Leftrightarrow x = \pm 3\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt. \( \Rightarrow \) Loại đáp án B. +) Xét đáp án C: \({x^2} - 7x + 4 = 0\) ta có: \(\Delta = {\left( { - 7} \right)^2} - 4.4 = 33 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt. \( \Rightarrow \) Loại đáp án C. +) Xét đáp án D: \({x^2} - 6x + 9 = 0\) ta có: \(\Delta ' = {3^2} - 9 = 0\) \( \Rightarrow \) Phương trình có nghiệm kép. \( \Rightarrow \) Chọn đáp án D. Chọn D. Câu 6 - Một số hệ thức về cạnh và góc trong tam giác vuông Phương pháp: Sử dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông để làm bài toán. Cách giải: Xét \(\Delta ABC\) vuông tại \(B\) ta có: \(AB = AC.\cos A\) \( = 10.\cos {60^0} = 10.\dfrac{1}{2} = 5\,cm\) Chọn C. Câu 7 - Vị trí tương đối của hai đường tròn Phương pháp: Cho hai đường tròn \(\left( {O;\,\,R} \right)\) và \(\left( {O';\,\,R'} \right)\) khi đó ta có: +) \(OO' > R + R'\) thì hai đường tròn nằm ngoài nhau hay hai đường tròn không có điểm chung. +) \(OO' < \left| {R - R'} \right|\) thì hai đường tròn đựng nhau hay hai đường tròn không có điểm chung. +) \(\left| {R - R'} \right| < OO' < R + R'\) thì hai đường tròn cắt nhau hay hai đường tròn có hai điểm chung. +) \(OO' = R + R'\) thì hai đường tròn tiếp xúc ngoài hay hai đường tròn có một điểm chung. +) \(OO' < \left| {R - R'} \right|\) thì hai đường tròn tiếp xúc trong hay hai đường tròn có một điểm chung. Cách giải: Ta có: \(OO' = 2cm = R' - R = 7cm - 5cm.\) \( \Rightarrow \left( {O;\,\,5cm} \right)\) và \(\left( {O';\,\,7cm} \right)\) tiếp xúc trong. Chọn B. Câu 8 - Hình trụ - Diện tích xung quanh và thể tích của Hình trụ Phương pháp: Diện tích xung quanh của hình trụ có bán kính đáy \(R\) và chiều cao \(h\) là: \({S_{xq}} = 2\pi Rh.\) Cách giải: Diện tích xung quanh của hình trụ đã cho là: \({S_{xq}} = 2\pi Rh = 2\pi .5.2 = 20\pi \,\,c{m^2}.\) Chọn A. Phần II: Tự luận Bài 1 - Rút gọn biểu thức chứa căn thức bậc hai Phương pháp: 1) Sử dụng các công thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\) và \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,khi\,\,A < 0\end{array} \right.,\,\,B \ge 0.\) 2) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức. Cách giải: 1) Chứng minh đẳng thức: \(\sqrt {{{\left( {\sqrt 5 - 4} \right)}^2}} - \sqrt 5 + \sqrt {20} = 4.\) Ta có: \(\begin{array}{l}\sqrt {{{\left( {\sqrt 5 - 4} \right)}^2}} - \sqrt 5 + \sqrt {20} \\ = \left| {\sqrt 5 - 4} \right| - \sqrt 5 + \sqrt {{2^2}.5} \\ = 4 - \sqrt 5 - \sqrt 5 + 2\sqrt 5 = 4.\end{array}\) Vậy \(\sqrt {{{\left( {\sqrt 5 - 4} \right)}^2}} - \sqrt 5 + \sqrt {20} = 4.\) 2) Rút gọn biểu thức: \(P = \left( {\dfrac{1}{{\sqrt x + 2}} + \dfrac{1}{{\sqrt x - 2}}} \right):\dfrac{2}{{x - 2\sqrt x }}\) với \(x > 0,\,\,x \ne 4.\) Điều kiện: \(x > 0,\,\,x \ne 4.\) \(\begin{array}{l}P = \left( {\dfrac{1}{{\sqrt x + 2}} + \dfrac{1}{{\sqrt x - 2}}} \right):\dfrac{2}{{x - 2\sqrt x }}\\\,\,\,\,\, = \dfrac{{\sqrt x - 2 + \sqrt x + 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}.\dfrac{{\sqrt x \left( {\sqrt x - 2} \right)}}{2}\\\,\,\,\,\, = \dfrac{{2\sqrt x }}{{\sqrt x + 2}}.\dfrac{{\sqrt x }}{2} = \dfrac{x}{{\sqrt x + 2}}.\end{array}\) Vậy với \(x > 0,\,\,x \ne 4\) thì \(P = \dfrac{x}{{\sqrt x + 2}}.\) Bài 2 - Hệ thức Vi-ét và ứng dụng Phương pháp: 1) Thay \(m = 4\) vào phương trình đã cho sau đó giải phương trình bậc hai một ẩn. 2) Phương trình \(a{x^2} + bx + c = 0\,\,\,\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \({x_1};\,\,{x_2}\) \( \Leftrightarrow \Delta > 0.\) Sử dụng hệ thức Vi-et: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\) và biểu thức bài cho để tìm \(m.\) Đối chiếu với điều kiện rồi kết luận. Cách giải: Cho phương trình: \({x^2} - \left( {2m + 1} \right)x + {m^2} + m = 0\) (với \(m\) là tham số). 1) Giải phương trình khi \(m = 4.\) Khi \(m = 4\) ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\,{x^2} - \left( {2.4 + 1} \right)x + {4^2} + 4 = 0\\ \Leftrightarrow {x^2} - 9x + 20 = 0\\ \Leftrightarrow {x^2} - 5x - 4x + 20 = 0\\ \Leftrightarrow x\left( {x - 5} \right) - 4\left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 5} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 4\end{array} \right.\end{array}\) Vậy với \(m = 4\) thì phương trình có tập nghiệm \(S = \left\{ {4;\,\,5} \right\}.\) 2) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt \({x_1};\,{x_2}\) với mọi \(m.\) Tìm \(m\) để \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 - 5{x_1}{x_2} = - 17.\) Xét phương trình \({x^2} - \left( {2m + 1} \right)x + {m^2} + m = 0\) có: \(\begin{array}{l}\Delta = {\left( {2m + 1} \right)^2} - 4\left( {{m^2} + m} \right)\\\,\,\,\,\, = 4{m^2} + 4m + 1 - 4{m^2} - 4m\\\,\,\,\,\, = 1 > 0\,\,\,\forall m\end{array}\) \( \Rightarrow \) Phương trình đã cho luôn có hai nghệm phân biệt \({x_1},\,\,{x_2}\) với mọi \(m.\) Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} + m\end{array} \right..\) Theo đề bài ta có: \(\begin{array}{l}\,\,\,\,\,\,x_1^2 + x_2^2 - 5{x_1}{x_2} = - 17\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 5{x_1}{x_2} = - 17\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 7{x_1}{x_2} = - 17\\ \Leftrightarrow {\left( {2m + 1} \right)^2} - 7\left( {{m^2} + m} \right) = - 17\\ \Leftrightarrow 4{m^2} + 4m + 1 - 7{m^2} - 7m = - 17\\ \Leftrightarrow 3{m^2} + 3m - 18 = 0\\ \Leftrightarrow {m^2} + m - 6 = 0\\ \Leftrightarrow {m^2} + 3m - 2m - 6 = 0\\ \Leftrightarrow m\left( {m + 3} \right) - 2\left( {m + 3} \right) = 0\\ \Leftrightarrow \left( {m + 3} \right)\left( {m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 3 = 0\\m - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 3\\m = 2\end{array} \right.\end{array}\) Vậy \(m = - 3\) và \(m = 2\) thỏa mãn bài toán. Bài 3 - Giải hệ phương trình bằng phương pháp cộng đại số Phương pháp: Đặt điều kiện để hệ phương trình xác định. Giải hệ phương trình bằng phương pháp đặt ẩn phụ. Giải hệ phương trình bằng phương pháp cộng đại số. Đối chiếu với điều kiện rồi kết luận. Cách giải: Giải hệ phương trình: \(\left\{ \begin{array}{l}2{\left( {x - 2} \right)^2} + \dfrac{1}{{\sqrt {y + 5} }} = 3\\{\left( {x - 2} \right)^2} - \dfrac{2}{{\sqrt {y + 5} }} = - 1\end{array} \right..\) ĐKXĐ: \(y > - 5\). Đặt \(u = {\left( {x - 2} \right)^2} \ge 0;\,\,v = \dfrac{1}{{\sqrt {y + 5} }} > 0\), hệ phương trình trở thành: \(\begin{array}{l}\left\{ \begin{array}{l}2u + v = 3\\u - 2v = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4u + 2v = 6\\u - 2v = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5u = 5\\v = 3 - 2u\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = 1\,\,\left( {tm} \right)\\v = 1\,\,\,\left( {tm} \right)\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}{\left( {x - 2} \right)^2} = 1\\\dfrac{1}{{\sqrt {y + 5} }} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x - 2 = 1\\x - 2 = - 1\end{array} \right.\\\sqrt {y + 5} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\\y + 5 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\\y = - 4\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) \in \left\{ {\left( {3; - 4} \right);\left( {1; - 4} \right)} \right\}\). Bài 4 - Ôn tập chương 3: Góc với đường tròn Cách giải: Cho \(\Delta ABC\) là tam giác nhọn nội tiếp đường tròn \(\left( {O;\,\,R} \right).\) Hai đường cao \(BD,\,\,CE\) của \(\Delta ABC\) cắt nhau tại \(H.\) Các tia \(BD,\,\,CE\) cắt đường tròn \(\left( {O;\,\,R} \right)\) lần lượt tại điểm thứ hai là \(P,\,Q.\) 1) Chứng minh tứ giác \(BCDE\) nội tiếp và \(cung\,\,AP = \,\,cung\,\,AQ.\) Ta cos: \(BD,\,CE\) là các đường cao của \(\Delta ABC\) \( \Rightarrow \left\{ \begin{array}{l}BD \bot AC = \left\{ D \right\}\\CE \bot AB = \left\{ E \right\}\end{array} \right.\) \( \Rightarrow \angle BEC = \angle BDC = {90^0}\) Xét tứ giác \(BEDC\) ta có: \(\angle BEC = \angle BDC = {90^0}\) Mà hai đỉnh \(E,\,\,D\) là hai đỉnh kề nhau \( \Rightarrow BEDC\) là tứ giác nội tiếp. (dhnb) Vì \(BEDC\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle EBD = \angle ECD\) (hai góc nội tiếp cùng chắn cung \(ED\)) \( \Rightarrow \angle ABP = \angle ACQ\) Lại có: \(\angle ABP,\,\,\angle ACQ\) lần lượt là các góc nội tiếp chắn các cung \(AP,\,\,AQ\) \( \Rightarrow cung\,\,\,AP = \,\,\,cung\,\,AQ\) (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau) (đpcm). 2) Chứng minh \(E\) là trung điểm của \(HQ\) và \(OA \bot DE.\) Xét tứ giác \(AEHD\) ta có: \(\angle AEH + \angle ADH = {90^0} + {90^0} = {180^0}\) Mà hai góc này là hai góc đối diện \( \Rightarrow AEHD\) là tứ giác nội tiếp. (dhnb) \( \Rightarrow \angle EAH = \angle EDH\) (hai góc nội tiếp cùng chắn cung \(EH\)). Vì \(BEDC\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle EDB = \angle ECB\) (hai góc nội tiếp cùng chắn cung \(EB\)) \( \Rightarrow \angle AEH = \angle ECB\,\,\left( { = \angle EDH} \right)\) Hay \(\angle EAH = \angle BAH = \angle BCQ\) Lại có: \(\angle QAB = \angle QCB\) (hai góc nội tiếp cùng chắn cung \(QB\)) \( \Rightarrow \angle EAH = \angle EAQ\,\,\left( { = \angle BCQ} \right)\) \( \Rightarrow AE\) là tia phân giác của \(\angle QAH.\) Xét \(\Delta QAH\) ta có: \(AE\) vừa là đường cao, vừa là đường phân giác \( \Rightarrow \Delta QAH\) cân tại \(A.\) (Tính chất tam giác cân) \( \Rightarrow AE\) cũng là đường trung tuyến của \(\Delta AQH.\) \( \Rightarrow E\) là trung điểm của \(HQ.\) (đpcm) Kéo dài \(AO\) cắt đường tròn \(\left( O \right)\) tại \(F.\) Khi đó ta có:\(\angle ABC = \angle AFC\) (hai góc nội tiếp cùng chắn cung \(AC\)) Vì \(BCDE\) là tứ giác nội tiếp (cmt) \( \Rightarrow \angle ADE = \angle ABC\) (góc ngoài tại một đỉnh bằng góc trong tại định đối diện) \( \Rightarrow \angle ADB = \angle AFC\left( { = \angle ABC} \right)\) Ta có: \(\angle ACF = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \(\begin{array}{l} \Rightarrow \angle CAF + \angle AFC = {90^0}\\ \Rightarrow \angle FAC + \angle ADE = {90^0}\end{array}\) Hay \(\angle DAO + \angle ADE = {90^0}\) \( \Rightarrow AO \bot DE\,\,\,\left( {dpcm} \right).\) 3) Cho \(CAB = {60^0},\,\,R = 6cm.\) Tính bán kính đường tròn ngoại tiếp \(\Delta AED.\) Theo chứng minh b) ta có: \(AEDH\) là tứ giác nội tiếp \( \Rightarrow \) Đường tròn ngoại tiếp \(\Delta AED\) là đường tròn ngoại tiếp tứ giác \(AEDH.\) Ta có: \(\angle AEH = {90^0}\) và là góc nội tiếp chắn cung \(AH\) \( \Rightarrow AH\) là đường kính của đường tròn ngoại tiếp tứ giác \(AEDH.\) Gọi \(J\) là tâm đường tròn ngoại tiếp \(\Delta ADE\) \( \Rightarrow J\) là trung điểm của \(AH.\) Gọi \(M\) là trung điểm của \(BC.\) Ta có: \(\left\{ \begin{array}{l}FC \bot AC\\DB \bot AC\end{array} \right. \Rightarrow FC//BD\) hay \(BH//FC.\) \(\left\{ \begin{array}{l}CE \bot AB\\BF \bot AB\end{array} \right. \Rightarrow CE//BF\) hay \(BF//CH.\) \( \Rightarrow BHCF\) là hình bình hành. \( \Rightarrow BC,\,\,HF\) cắt nhau tại trung điểm của mỗi đường Mà \(M\) là trung điểm của \(BC\) \( \Rightarrow M\) cũng là trung điểm của \(HF.\) Xét \(\Delta AHF\) ta có: \(O,\,\,M\) lần lượt là trung điểm của \(AF,\,\,HF\) \( \Rightarrow OM\) là đường trung bình của \(\Delta AHF\) \( \Rightarrow \left\{ \begin{array}{l}OM//AH\\OM = \dfrac{1}{2}AH\end{array} \right..\) Ta có: \(\angle BOC\) là góc ở tâm chắn cung \(BC\) \(\angle BAC\) là góc ở tâm chắn cung \(BC\) \( \Rightarrow \angle BOC = 2\angle BAC = {2.60^0} = {120^0}\) \(\Delta OBC\) cân tại \(O\) có đường trung tuyến \(OM\) \( \Rightarrow OM\) cũng là phân giác của \(\angle BOC\) \( \Rightarrow \angle BOM = {60^0}.\) Xét \(\Delta OBM\) ta có: \(OM = OB.\cos \angle BOM = 6.\cos {60^0} = 3cm.\) \( \Rightarrow AH = 2OM = 2.3 = 6cm.\) Vậy bán kính của đường tròn ngoại tiếp \(\Delta ADE\) là: \(AJ = \dfrac{1}{2}AH = 3cm.\) Bài 5 Phương pháp: 1) Tìm điều kiện xác định của phương trình. Biến đổi để đưa phương trình về dạng phương trình tích rồi giải phương trình. Đối chiếu với điều kiện rồi kết luận. 2) Sử dụng bất đẳng thức Cô-si để chứng minh. Cách giải: 1) Giải phương trình: \(\sqrt 2 \sqrt {2{x^2} + x + 1} - \sqrt {4x - 1} + 2{x^2} + 3x - 3 = 0.\) Điều kiện: \(x \ge \dfrac{1}{4}\) \(\begin{array}{l}\,\,\,\,\,\,\sqrt 2 \sqrt {2{x^2} + x + 1} - \sqrt {4x - 1} + 2{x^2} + 3x - 3 = 0\\ \Leftrightarrow \sqrt {4{x^2} + 2x + 2} - 2 + 1 - \sqrt {4x - 1} + 2{x^2} + 3x - 2 = 0\\ \Leftrightarrow \dfrac{{4{x^2} + 2x + 2 - 4}}{{\sqrt {4{x^2} + 2x + 2} + 2}} + \dfrac{{1 - 4x + 1}}{{1 + \sqrt {4x - 1} }} + 2{x^2} + 4x - x - 2 = 0\\ \Leftrightarrow \dfrac{{4{x^2} + 2x - 2}}{{\sqrt {4{x^2} + 2x + 2} + 2}} + \dfrac{{2 - 4x}}{{1 + \sqrt {4x - 1} }} + 2x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \dfrac{{2\left( {2{x^2} + x - 1} \right)}}{{\sqrt {4{x^2} + 2x + 2} + 2}} + \dfrac{{2\left( {1 - 2x} \right)}}{{1 + \sqrt {4x - 1} }} + \left( {x + 2} \right)\left( {2x - 1} \right) = 0\\ \Leftrightarrow \dfrac{{2\left( {2x - 1} \right)\left( {x + 1} \right)}}{{\sqrt {4{x^2} + 2x + 2} + 2}} - \dfrac{{2\left( {2x - 1} \right)}}{{1 + \sqrt {4x - 1} }} + \left( {x + 2} \right)\left( {2x - 1} \right) = 0\end{array}\) \(\begin{array}{l} \Leftrightarrow \left( {2x - 1} \right)\left[ {\dfrac{{2x + 1}}{{\sqrt {4{x^2} + 2x + 2} + 2}} - \dfrac{2}{{\sqrt {4x - 1} + 1}} + x + 2} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x - 1 = 0\\\dfrac{{2x + 1}}{{\sqrt {4{x^2} + 2x + 2} + 2}} - \dfrac{2}{{\sqrt {4x - 1} + 1}} + x + 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\,\,\,\left( {tm} \right)\\\dfrac{{2x + 1}}{{\sqrt {4{x^2} + 2x + 2} + 2}} + x + 2 - \dfrac{2}{{\sqrt {4x - 1} + 1}} = 0\,\,\,\,\left( * \right)\end{array} \right.\end{array}\) Với \(x \ge \dfrac{1}{4} \Rightarrow \sqrt {4x - 1} + 1 \ge 1\) \( \Rightarrow \dfrac{2}{{\sqrt {4x - 1} + 1}} \le 2\) \(\begin{array}{l} \Rightarrow 2 - \dfrac{2}{{\sqrt {4x - 1} + 1}} \ge 0\\ \Rightarrow \dfrac{{2x + 1}}{{\sqrt {4{x^2} + 2x + 2} + 2}} + x + 2 - \dfrac{2}{{\sqrt {4x - 1} + 1}} > 0\,\,\,\forall x \ge \dfrac{1}{4}\end{array}\) \( \Rightarrow \left( * \right)\) vô nghiệm. Vậy phương trình có nghiệm duy nhất \(x = \dfrac{1}{2}.\) 2) Cho các số thực dương \(a,\,\,b,\,\,c\) thỏa mãn: \(ab + bc + ca = 3.\) Chứng minh: \(\dfrac{{{a^3}}}{{b + 2c}} + \dfrac{{{b^3}}}{{c + 2a}} + \dfrac{{{c^3}}}{{a + 2b}} \ge 1.\) Sưu tầm: Facebook. Đặt \(P = \dfrac{{{a^3}}}{{b + 2c}} + \dfrac{{{b^3}}}{{c + 2a}} + \dfrac{{{c^3}}}{{a + 2b}}\) Áp dụng bất đẳng thức Cô-si cho hai số dương \(\dfrac{{9{a^3}}}{{b + 2c}};\,\,\,\left( {b + 2c} \right)a\) ta có: \(\dfrac{{9{a^2}}}{{b + 2c}} + \left( {b + 2c} \right)a \ge 6{a^2}\) Tương tự ta có: \(\left\{ \begin{array}{l}\dfrac{{9{b^3}}}{{c + 2a}} + \left( {c + 2a} \right)b \ge 6{b^2}\\\dfrac{{9{c^3}}}{{a + 2b}} + \left( {a + 2b} \right)c \ge 6{c^2}\end{array} \right.\) Cộng vế với vế ba bất đẳng thức cùng chiều ta có: \(\begin{array}{l}9\left( {\dfrac{{{a^3}}}{{b + 2c}} + \dfrac{{{b^3}}}{{c + 2a}} + \dfrac{{{c^3}}}{{a + 2b}}} \right) + \left( {b + 2c} \right)a + \left( {c + 2a} \right)b + \left( {a + 2b} \right)c \ge 6{a^2} + 6{b^2} + 6{c^2}\\ \Leftrightarrow 9P + 3\left( {ab + bc + ca} \right) \ge 6\left( {{a^2} + {b^2} + {c^2}} \right)\\ \Leftrightarrow 9P + 9 \ge 6\left( {{a^2} + {b^2} + {c^2}} \right)\\ \Leftrightarrow 3P + 3 \ge 2\left( {{a^2} + {b^2} + {c^2}} \right)\end{array}\) Lại có: \({a^2} + {b^2} + {c^2} \ge ab + bc + ca = 3\) \(\begin{array}{l} \Rightarrow 3P \ge 2.3 - 3 = 3\\ \Leftrightarrow P \ge 1.\end{array}\) Vậy \(\dfrac{{{a^3}}}{{b + 2c}} + \dfrac{{{b^3}}}{{c + 2a}} + \dfrac{{{c^3}}}{{a + 2b}} \ge 1.\
|