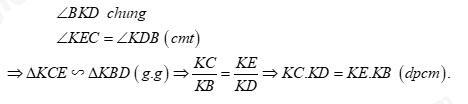Đề thi vào 10 môn Toán Thái Bình năm 2019

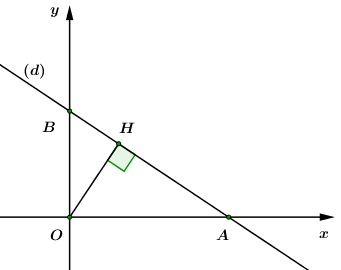
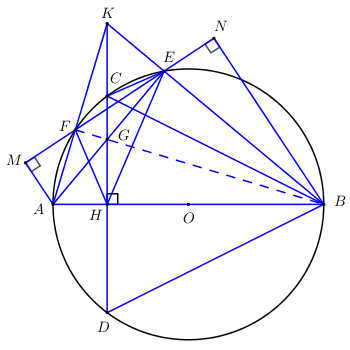
Đề bài

Câu 1 (2 điểm):

Cho $A = \dfrac{{x + \sqrt x  + 1}}{{\sqrt x  + 1}}$ và $B = \dfrac{1}{{\sqrt x  - 1}} - \dfrac{{x + 2}}{{x\sqrt x  - 1}} - \dfrac{{\sqrt x  + 1}}{{x + \sqrt x  + 1}}$ với $x \ge 0,\,\,x \ne 1.$

a) Tính giá trị của biểu thức $A$ khi $x = 2.$ 

b) Rút gọn biểu thức $B.$

c) Tìm $x$ sao cho biểu thức $C =  - A.B$ nhận giá trị là số nguyên.

Câu 2 (2 điểm):

a. Giải hệ phương trình: $\left\{ \begin{array}{l}4x + y = 3\\2x - y = 1\end{array} \right.$ (không sử dụng máy tính cầm tay).

b. Một mảnh vườn hình chữ nhật có diện tích 150 m^2. Biết rằng, chiều dài mảnh vườn hơn chiều chiều rộng mảnh vườn là 5m. Tính chiều rộng mảnh vườn.

Câu 3 (2 điểm)  Cho hàm số $y = \left( {m - 4} \right)x + m + 4\,\,$ (m là tham số)

a. Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên R.

b. Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol $\left( P \right):\,\,\,y = {x^2}$  tại hai điểm phân biệt. Gọi ${x_1},{x_2}$ là hoành độ các giao điểm, tìm m sao cho ${x_1}.\left( {{x_1} - 1} \right) + {x_2}\left( {{x_2} - 1} \right) = 18$

c. Gọi đồ thị hàm số đã cho là đường thẳng $\left( d \right)$ . Chứng minh  khoảng cách từ điểm $O\left( {0;0} \right)$ đến $\left( d \right)$ không lớn hơn $\sqrt {65} .$

Câu 4 (3,5 điểm):  Cho đường tròn tâm $O$, đường kính $AB$. Kẻ dây cung $CD$ vuông góc với $AB$ tại $H$ ($H$ nằm giữa $A$ và $O$, $H$ khác $A$ và $O$). Lấy điểm $G$ thuộc đoạn $CH$ ($G$ khác $C$ và $H$), tia $AG$ cắt đường tròn tại $E$ khác $A$.

a. Chứng minh tứ giác $BEGH$ là tứ giác nội tiếp.

b. Gọi $K$ là giao điểm của hai đường thẳng $BE$ và $CD$. Chứng minh $KC.KD = KE.KB$.

c. Đoạn thẳng $AK$ cắt đường tròn tâm $O$ tại $F$ khác $A$. Chứng minh $G$ là tâm đường tròn nội tiếp tam giác $HEF$.

d. Gọi $M,\,\,N$ lần lượt là hình chiếu vuông góc của $A$ và $B$ lên đường thẳng $EF$. Chứng minh $HE + HF = MN$.

Câu 5 (0,5 điểm)

Cho $a,\,\,b,\,\,c$ là các số thực dương thỏa mãn $a + b + c + ab + bc + ca = 6$. Chứng minh rằng $\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge 3$. 

Lời giải chi tiết

Câu 1 (2 điểm)

Phương pháp:

a) Thay giá trị $x = 2\,\,\,\left( {tmdk} \right)$ vào biểu thức $A$ và tính giá trị của biểu thức.

b) Quy đồng mẫu, biến đổi và rút gọn biểu thức.

c) Tính biểu thức $C,$ đánh giá giá trị của biểu thức $C$ sau đó tìm $x$ để $C \in \mathbb{Z}.$

Đối chiếu với điều kiện rồi kết luận.

Cách giải:

Cho $A = \dfrac{{x + \sqrt x  + 1}}{{\sqrt x  + 1}}$ và $B = \dfrac{1}{{\sqrt x  - 1}} - \dfrac{{x + 2}}{{x\sqrt x  - 1}} - \dfrac{{\sqrt x  + 1}}{{x + \sqrt x  + 1}}$ với $x \ge 0,\,\,x \ne 1.$

a) Tính giá trị của biểu thức $A$ khi $x = 2.$ 

Điều kiện: $x \ge 0,\,\,\,x \ne 1.$

Khi $x = 2\,\,\,\left( {tmdk} \right)$ ta thay vào biểu thức $A$ ta được:

$A = \dfrac{{2 + \sqrt 2  + 1}}{{\sqrt 2  + 1}} = \dfrac{{3 + \sqrt 2 }}{{\sqrt 2  + 1}} = \dfrac{{\left( {3 + \sqrt 2 } \right)\left( {\sqrt 2  - 1} \right)}}{{\left( {\sqrt 2  + 1} \right)\left( {\sqrt 2  - 1} \right)}} = \dfrac{{3\sqrt 2  - 3 + 2 - \sqrt 2 }}{{2 - 1}} = 2\sqrt 2  - 1.$

Vật với $x = 2$ thì $A = 2\sqrt 2  - 1.$

b) Rút gọn biểu thức $B.$

Điều kiện: $x \ge 0,\,\,\,x \ne 1.$

$\begin{array}{l}B = \dfrac{1}{{\sqrt x  - 1}} - \dfrac{{x + 2}}{{x\sqrt x  - 1}} - \dfrac{{\sqrt x  + 1}}{{x + \sqrt x  + 1}}\\\,\,\,\, = \dfrac{1}{{\sqrt x  - 1}} - \dfrac{{x + 2}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}} - \dfrac{{\sqrt x  + 1}}{{x + \sqrt x  + 1}}\\\,\,\, = \dfrac{{x + \sqrt x  + 1 - x - 2 - \left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}\\\,\,\, = \dfrac{{\sqrt x  - 1 - x + 1}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}} = \dfrac{{\sqrt x  - x}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}\\\,\,\, = \dfrac{{\sqrt x \left( {1 - \sqrt x } \right)}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}} = \dfrac{{ - \sqrt x }}{{x + \sqrt x  + 1}}.\end{array}$

c) Tìm $x$ sao cho biểu thức $C =  - A.B$ nhận giá trị là số nguyên.

Điều kiện: $x \ge 0,\,\,\,x \ne 1.$

Ta có: $C =  - A.B$

$\Rightarrow C =  - \dfrac{{x + \sqrt x  + 1}}{{\sqrt x  + 1}}.\dfrac{{ - \sqrt x }}{{x + \sqrt x  + 1}} = \dfrac{{\sqrt x }}{{\sqrt x  + 1}} = \dfrac{{\sqrt x  + 1 - 1}}{{\sqrt x  + 1}} = 1 - \dfrac{1}{{\sqrt x  + 1}}.$

Với $x \ge 0,\,\,x \ne 1 \Rightarrow \sqrt x  + 1 > 0 \Rightarrow \left\{ \begin{array}{l}C = \dfrac{{\sqrt x }}{{\sqrt x  + 1}} \ge 0\\C = \dfrac{{\sqrt x }}{{\sqrt x  + 1}} = 1 - \dfrac{1}{{\sqrt x  + 1}} < 1\end{array} \right. \Rightarrow 0 \le C < 1.$

$\Rightarrow C \in \mathbb{Z} \Leftrightarrow C = 0 \Leftrightarrow \dfrac{{\sqrt x }}{{\sqrt x  + 1}} = 0 \Leftrightarrow \sqrt x  = 0 \Leftrightarrow x = 0\,\,\,\left( {tm} \right).$

Vậy $x = 0$ thì $C =  - A.B$ nhận giá trị nguyên.

Câu 2 (2,0 điểm)

Phương pháp:

a) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.

b) Giải bài toán bằng cách lập phương trình:

Gọi chiều rộng mảnh vườn hình chữ nhật là: $x\,\,\,\left( m \right),\,\,x > 0.$

Khi đó chiều dài mảnh vườn là: $x + 5\left( m \right)$

Dựa vào giả thiết bài toán để lập phương trình.

Giải phương trình, đối chiếu với điều kiện rồi kết luận.

Cách giải:

a. Giải hệ phương trình: $\left\{ \begin{array}{l}4x + y = 3\\2x - y = 1\end{array} \right.$

$\left\{ \begin{array}{l}4x + y = 3\\2x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x = 4\\2x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{3}\\2.\dfrac{2}{3} - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{3}\\y = \dfrac{1}{3}\end{array} \right.$

Vậy hệ phương trình có nghiệm duy nhất là: $\left( {x;y} \right) = \left( {\dfrac{2}{3};\dfrac{1}{3}} \right)$.

b. Một mảnh vườn hình chữ nhật có diện tích 150 m^2. Biết rằng, chiều dài mảnh vườn hơn chiều chiều rộng mảnh vườn là 5m. Tính chiều rộng mảnh vườn.

Gọi chiều rộng mảnh vườn hình chữ nhật là: $x\,\,\,\left( m \right),\,\,x > 0.$

Khi đó chiều dài mảnh vườn là: $x + 5\left( m \right)$

Diện tích mảnh vườn hình chữ nhật là $150\,{m^2}$ nên ta có phương trình:

$\begin{array}{l}\,\,\,\,\,\,\,x\left( {x + 5} \right) = 150\\ \Leftrightarrow {x^2} + 5x - 150 = 0\\ \Leftrightarrow {x^2} + 15x - 10x - 150 = 0\\ \Leftrightarrow \left( {x + 15} \right)\left( {x - 10} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 15 = 0\\x - 10 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 15\,\,\,\left( {ktm} \right)\\x = 10\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Vậy chiều rộng của mảnh vườn hình chữ nhật là 10m.

Câu 3 (2,0 điểm)

Phương pháp:

a) Hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ đồng biến $\Leftrightarrow a > 0.$

b) Lập phương trình hoành độ giao điểm của hai đồ thị hàm số.

$d$ cắt $\left( P \right)$ tại hai điểm phân biệt $\Leftrightarrow$ phương trình hoành độ giao điểm có hai nghiệm phân biệt $\Leftrightarrow \Delta  > 0\,\,\,\left( {\Delta ' > 0} \right).$

Áp dụng định lý Vi-et để tìm $m.$

c) Vẽ đồ thị hàm số, sử dụng hệ thức lượng trong tam giác vuông để chứng minh bài toán.

Cách giải:

Cho hàm số $y = \left( {m - 4} \right)x + m + 4\,\,$ (m là tham số)

a. Tìm m để hàm số đã cho là hàm số bậc nhất đồng biến trên R.

Hàm số đã cho là hàm số bậc nhất đồng biến trên R khi $\left\{ \begin{array}{l}m - 4 \ne 0\\m - 4 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\m > 4\end{array} \right. \Leftrightarrow m > 4.$

b. Chứng minh rằng với mọi giá trị của m thì đồ thị hàm số đã cho luôn cắt parabol $\left( P \right):y = {x^2}$  tại hai điểm phân biệt. Gọi ${x_1},{x_2}$ là hoành độ các giao điểm, tìm m sao cho ${x_1}.\left( {{x_1} - 1} \right) + {x_2}\left( {{x_2} - 1} \right) = 18$

Gọi đồ thị hàm số $y = \left( {m - 4} \right)x + m + 4\,\,$ là đường thẳng (d).

Xét phương trình hoành độ giao điểm của đồ thị hàm số (d) và parabol (P):

${x^2} = \left( {m - 4} \right)x + m + 4\,\, \Leftrightarrow {x^2} - \left( {m - 4} \right)x - m - 4 = 0\,\,\,\left( * \right)$

Số giao điểm của (d) và  (P) đồng thời cũng là số nghiệm của phương trình (*).

Có các hệ số: $a = 1;\,\,\,b =  - \left( {m - 4} \right);\,\,\,c =  - m - 4$.

Ta có: $\Delta  = {\left( {m - 4} \right)^2} + 4\left( {m + 4} \right) = {m^2} - 8m + 16 + 4m + 16 = {m^2} - 4m + 4 + 28 = {\left( {m - 2} \right)^2} + 28$

Ta có: ${\left( {m - 2} \right)^2} \ge 0,\forall m \Rightarrow {\left( {m - 2} \right)^2} + 28 > 0,\forall m\,\,\,hay\,\,\Delta  > 0,\forall m$ .

Vậy phương trình (*) luôn có hai nghiệm phân biệt ${x_1},{x_2}$  hay (d) và (P) luôn cắt nhau tại hai điểm phân biệt.

Áp dụng hệ thức Vi-et cho phương trình  (*) ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = m - 4\\{x_1}{x_2} =  - m - 4\end{array} \right.$

Theo đề ra ta có:

 $\begin{array}{l}\,\,\,\,\,\,{x_1}.\left( {{x_1} - 1} \right) + {x_2}\left( {{x_2} - 1} \right) = 18\\ \Leftrightarrow x_1^2 - {x_1} + x_2^2 - {x_2} - 18 = 0\\ \Leftrightarrow \left( {x_1^2 + x_2^2} \right) - \left( {{x_1} + {x_2}} \right) - 18 = 0\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) - 18 = 0\\ \Leftrightarrow {\left( {m - 4} \right)^2} - 2\left( { - m - 4} \right) - \left( {m - 4} \right) - 18 = 0\\ \Leftrightarrow {m^2} - 8m + 16 + 2m + 8 - m + 4 - 18 = 0\\ \Leftrightarrow {m^2} - 7m + 10 = 0\\ \Leftrightarrow {m^2} - 2m - 5m + 10 = 0\\ \Leftrightarrow m\left( {m - 2} \right) - 5\left( {m - 2} \right) = 0\\ \Leftrightarrow \left( {m - 2} \right)\left( {m - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 2 = 0\\m - 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 2\,\,\left( {tm} \right)\\m = 5\,\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Vậy $m = 2,\,\,m = 5$ là giá trị thỏa mãn yêu cầu bài toán.

c. Gọi đồ thị hàm số đã cho là đường thẳng $\left( d \right).$ Chứng minh khoảng cách từ điểm $O\left( {0;\,\,0} \right)$ đến $\left( d \right)$ không lớn hơn $\sqrt {65} .$

Ta có: $\left( d \right):\,\,\,y = \left( {m - 4} \right)x + m + 4.$

+) Xét TH $m - 4 = 0 \Leftrightarrow m = 4$ ta có: $\left( d \right):\,\,\,y = 8$  là đường thẳng song song với trục hoành

$\Rightarrow d\left( {O;\,\,\left( d \right)} \right) = 8 = \sqrt {64}  < \sqrt {65} .$

$\Rightarrow d\left( {O;\,\,\left( d \right)} \right) < \sqrt {65}$ với $m = 4.$

+) Xét TH $m - 4 \ne 0 \Leftrightarrow m \ne 4$ ta có:

Gọi $A$  giao điểm của đường thẳng $\left( d \right)$ với trục $Ox \Rightarrow A\left( {{x_A};\,\,0} \right).$ 

$\begin{array}{l} \Rightarrow 0 = \left( {m - 4} \right){x_A} + m + 4 \Leftrightarrow {x_A} =  - \dfrac{{m + 4}}{{m - 4}} \Rightarrow A\left( { - \dfrac{{m + 4}}{{m - 4}};\,\,0} \right)\\ \Rightarrow OA = \left| {{x_A}} \right| = \left| { - \dfrac{{m + 4}}{{m - 4}}} \right| = \left| {\dfrac{{m + 4}}{{m - 4}}} \right|.\end{array}$

Gọi $B$  giao điểm của đường thẳng $\left( d \right)$ với trục $Oy \Rightarrow B\left( {0;\,\,{y_B}} \right)$

$\begin{array}{l} \Rightarrow {y_B} = \left( {m - 4} \right).0 + m + 4 = m + 4 \Rightarrow B\left( {0;\,\,m + 4} \right).\\ \Rightarrow OB = \left| {{y_B}} \right| = \left| {m + 4} \right|.\end{array}$

Gọi $H$ là chân đường vuông góc hạ từ $O$ đến đường thẳng $\left( d \right).$ Khi đó ta có: $d\left( {O;\,\,\left( d \right)} \right) = OH.$

Áp dụng hệ thức lượng cho $\Delta OAB$ vuông tại $O$ có đường cao $OH$ ta có:

$\begin{array}{l}\,\,\,\,\,\,\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{{{{\left( {\left| {\dfrac{{m + 4}}{{m - 4}}} \right|} \right)}^2}}} + \dfrac{1}{{{{\left( {\left| {m + 4} \right|} \right)}^2}}}\\ \Leftrightarrow \dfrac{1}{{O{H^2}}} = \dfrac{{{{\left( {m - 4} \right)}^2}}}{{{{\left( {m + 4} \right)}^2}}} + \dfrac{1}{{{{\left( {m + 4} \right)}^2}}} = \dfrac{{{{\left( {m - 4} \right)}^2} + 1}}{{{{\left( {m + 4} \right)}^2}}}\\ \Leftrightarrow O{H^2} = \dfrac{{{{\left( {m + 4} \right)}^2}}}{{{{\left( {m - 4} \right)}^2} + 1}}.\end{array}$

Giả sử khoảng cách từ $O$ đến đường thẳng $\left( d \right)$ không lớn hơn $\sqrt {65}  \Leftrightarrow d\left( {O;\,\,\left( d \right)} \right) \le \sqrt {65}$

$\begin{array}{l} \Leftrightarrow OH \le \sqrt {65}  \Leftrightarrow O{H^2} \le 65\\ \Leftrightarrow \dfrac{{{{\left( {m + 4} \right)}^2}}}{{{{\left( {m - 4} \right)}^2} + 1}} \le 65\\ \Leftrightarrow {\left( {m + 4} \right)^2} \le 65\left[ {{{\left( {m - 4} \right)}^2} + 1} \right]\,\,\,\,\left( {do\,\,{{\left( {m - 4} \right)}^2} + 1 > 0} \right)\\ \Leftrightarrow {m^2} + 8m + 16 \le 65{m^2} - 520m + 1105\\ \Leftrightarrow 64{m^2} - 528m + 1089 \ge 0\\ \Leftrightarrow 64{m^2} - 2.8m.33 + {33^2} \ge 0\\ \Leftrightarrow {\left( {8m - 33} \right)^2} \ge 0\,\,\,\end{array}$

Ta có: ${\left( {8m - 33} \right)^2} \ge 0\,\,\forall m \Rightarrow O{H^2} \le 65\,\,\,\forall m \Rightarrow d\left( {O;\,\,\left( d \right)} \right) = OH \le \sqrt {65}$

$\Rightarrow d\left( {O;\,\,\left( d \right)} \right)$ không lớn $\sqrt {65}$ với mọi $m \ne 4.$

Kết hợp hai trường hợp trên ta được khoảng cách từ $O$ đến đường thẳng $\left( d \right)$ không lớn hơn $\sqrt {65} .$

Câu 4 (3,5 điểm)

Phương pháp:

a) Sử dụng các dấu hiệu nhận biết để chứng minh tứ giác nội tiếp.

b) Chứng minh các tam giác đồng dạng để từ đó suy ra đẳng thức cần chứng minh.

c) Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường phân giác.

Cách giải:

Cho đường tròn tâm $O$, đường kính $AB$. Kẻ dây cung $CD$ vuông góc với $AB$ tại $H$ ($H$ nằm giữa $A$ và $O$, $H$ khác $A$ và $O$). Lấy điểm $G$ thuộc đoạn $CH$ ($G$ khác $C$ và $H$), tia $AG$ cắt đường tròn tại $E$ khác $A$.

a. Chứng minh tứ giác $BEGH$ là tứ giác nội tiếp.

Ta có $\angle AEB = {90^0}$ (góc nội tiếp chắn nửa đường tròn $\left( O \right)$) $\Rightarrow \angle GEB = {90^0}$.

Có $CD \bot AB$ tại $H\,\,\left( {gt} \right) \Rightarrow \angle GHB = {90^0}$

Xét tứ giác $BEGH$ có: $\angle GHB + \angle GEB = {90^0} + {90^0} = {180^0} \Rightarrow$ Tứ giác $BEGH$ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng ${180^0}$).

b. Gọi $K$ là giao điểm của hai đường thẳng $BE$ và $CD$. Chứng minh $KC.KD = KE.KB$.

Dễ thấy tứ giác $BECD$ nội tiếp đường tròn $\left( O \right) \Rightarrow \angle KEC = \angle CDB = \angle KDB$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).

Xét tam giác $KCE$ và tam giác $KBD$ có:

c. Đoạn thẳng $AK$ cắt đường tròn tâm $O$ tại $F$ khác $A$. Chứng minh $G$ là tâm đường tròn nội tiếp tam giác $HEF$.

Ta có: $\angle AFB = {90^0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow BF \bot AF$ (1).

Xét tam giác $KAB$ có hai đường cao $AE$ và $KH$ cắt nhau tại $G \Rightarrow G$ là trực tâm của tam giác $KAB$.

$\Rightarrow BG \bot AK$ hay $BG \bot AF$ (2)

Từ (1) và (2) $\Rightarrow$ qua $B$ kẻ được 2 đường thẳng $BG$ và $BF$ cùng vuông góc với $AF$.

$\Rightarrow BG \equiv BF$ hay $B,\,\,G,\,\,F$ thẳng hàng $\Rightarrow GF \bot AF \Rightarrow \angle AFG = {90^0}$.

Xét tứ giác $AFGH$ có: $\angle AFG + \angle AHG = {90^0} + {90^0} = {180^0} \Rightarrow$ Tứ giác $AFGH$ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng ${180^0}$).

$\Rightarrow \angle GHF = \angle GAF$ (hai góc nội tiếp cùng chắn cung $GF$).

Tứ giác $BEGH$ nội tiếp (cmt) $\Rightarrow GHE = \angle GBE$ (hai góc nội tiếp cùng chắn cung $GE$).

Lại có $\angle GAF = \angle EAF = \angle EBF = \angle GBE$ (hai góc nội tiếp cùng chắn cung $EF$).

$\Rightarrow \angle GHF = \angle GHE \Rightarrow HG$ là phân giác của $\angle EHF$ (*)

Tứ giác $BEGH$ nội tiếp (cmt) $\Rightarrow \angle GEH = \angle GBH$ (hai góc nội tiếp cùng chắn cung $GH$).

Mà $\angle GBH = \angle FBA = \angle FEA = \angle GEF$ (hai góc nội tiếp cùng chắn cung $AF$)

$\Rightarrow \angle GEH = \angle GEF \Rightarrow EG$ là phân giác của $\angle HEF$ (**)

Từ (*) và (**) $\Rightarrow G$ là giao điểm của hai đường phân giác của tam giác $HEF \Rightarrow G$ là tâm đường tròn nội tiếp tam giác $HEF$.

Câu 5 (0,5 điểm)

Phương pháp:

Sử dụng bất đẳng thức Cô-si để chứng minh.

Cách giải:

Ta có:

$\begin{array}{l}a + b + c + ab + bc + ca = 6 \Leftrightarrow a + b + c = 6 - \left( {ab + bc + ca} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}6 - \left( {ab + bc + ca} \right) > 0\\{\left( {a + b + c} \right)^2} = {\left[ {6 - \left( {ab + bc + ca} \right)} \right]^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}ab + bc + ca < 6\\\left( {{a^2} + {b^2} + {c^2}} \right) + 2\left( {ab + bc + ca} \right) = 36 - 12\left( {ab + bc + ca} \right) + {\left( {ab + bc + ca} \right)^2}\,\,\,\left( 1 \right)\end{array} \right.\end{array}$

Áp dụng BĐT Cô-si ta có: $\left\{ \begin{array}{l}ab \le \dfrac{{{a^2} + {b^2}}}{2}\\bc \le \dfrac{{{b^2} + {c^2}}}{2}\\ca \le \dfrac{{{c^2} + {a^2}}}{2}\end{array} \right. \Rightarrow ab + bc + ca \le \dfrac{{{a^2} + {b^2} + {b^2} + {c^2} + {c^2} + {a^2}}}{2} = {a^2} + {b^2} + {c^2}$

$\begin{array}{l} \Rightarrow VT\left( 1 \right) \ge ab + bc + ca + 2\left( {ab + bc + ca} \right) = 3\left( {ab + bc + ca} \right)\\ \Rightarrow 36 - 12\left( {ab + bc + ca} \right) + {\left( {ab + bc + ca} \right)^2} \ge 3\left( {ab + bc + ca} \right)\end{array}$

Đặt $t = ab + bc + ca\,\,\,\left( {0 < t < 6} \right)$ ta có :

$\begin{array}{l}36 - 12t + {t^2} \ge 3t \Leftrightarrow {t^2} - 15t + 36 \ge 0 \Leftrightarrow {t^2} - 12t - 3t + 36 \ge 0\\ \Leftrightarrow t\left( {t - 12} \right) - 3\left( {t - 12} \right) \ge 0 \Leftrightarrow \left( {t - 12} \right)\left( {t - 3} \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}t \ge 12\\t \le 3\end{array} \right.\end{array}$

Kết hợp điều kiện $0 < t < 6 \Rightarrow 0 < t \le 3$.

Theo bài ra ta có :

$\dfrac{{{a^3}}}{b} + \dfrac{{{b^3}}}{c} + \dfrac{{{c^3}}}{a} \ge 3 \Leftrightarrow \dfrac{{{a^3}}}{b} + ab + \dfrac{{{b^3}}}{c} + bc + \dfrac{{{c^3}}}{a} + ca \ge 3 + \left( {ab + bc + ca} \right)$.

Áp dụng BĐT Cô-si ta có: $\dfrac{{{a^3}}}{b} + ab \ge 2\sqrt {\dfrac{{{a^3}}}{b}.ab}  = 2{a^2}$.

Tương tự : $\dfrac{{{b^3}}}{c} + bc \ge 2{b^2};\,\,\dfrac{{{c^3}}}{a} + ac \ge 2{c^2}$.

$\Rightarrow \dfrac{{{a^3}}}{b} + ab + \dfrac{{{b^3}}}{c} + bc + \dfrac{{{c^3}}}{a} + ca \ge 2\left( {{a^2} + {b^2} + {c^2}} \right)$.

Ta cần chứng minh $2\left( {{a^2} + {b^2} + {c^2}} \right) \ge 3 + \left( {ab + bc + ca} \right)$.

$\begin{array}{l} \Leftrightarrow 2\left[ {{{\left( {a + b + c} \right)}^2} - 2\left( {ab + bc + ca} \right)} \right] \ge 3 + \left( {ab + bc + ca} \right)\\ \Leftrightarrow 2\left[ {{{\left( {6 - \left( {ab + bc + ca} \right)} \right)}^2} - 2\left( {ab + bc + ca} \right)} \right] \ge 3 + \left( {ab + bc + ca} \right)\\ \Leftrightarrow 2\left[ {{{\left( {6 - t} \right)}^2} - 2t} \right] \ge 3 + t\,\,\left( {0 < t \le 3} \right)\\ \Leftrightarrow 2\left( {36 - 12t + {t^2} - 2t} \right) \ge 3 + t\\ \Leftrightarrow 72 - 24t + 2{t^2} - 4t - 3 - t \ge 0\\ \Leftrightarrow 2{t^2} - 29t + 69 \ge 0\\ \Leftrightarrow 2{t^2} - 6t - 23t + 69 \ge 0\\ \Leftrightarrow 2\left( {t - 3} \right) - 23\left( {t - 3} \right) \ge 0\\ \Leftrightarrow \left( {t - 3} \right)\left( {2t - 23} \right) \ge 0\end{array}$

Với $0 < t \le 3\,\,\left( {cmt} \right) \Rightarrow \left\{ \begin{array}{l}t - 3 \le 0\\2t \le 6 \Leftrightarrow 2t - 23 \le  - 17 < 0\end{array} \right. \Rightarrow \left( {t - 3} \right)\left( {2t - 23} \right) \ge 0$.

Vậy đẳng thức được chứng minh.  Dấu "=" xảy ra $\Leftrightarrow a = b = c = 1$.