Đề thi vào 10 môn Toán Thanh Hóa năm 2021

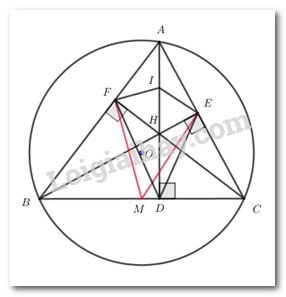
Đề bài

Câu I (2,0 điểm):

Cho biểu thức $P = \dfrac{{\sqrt x }}{{\sqrt x  + 5}} + \dfrac{{2\sqrt x }}{{\sqrt x  - 5}} - \dfrac{{3x + 25}}{{x - 25}}$ với $x \ge 0,\,\,x \ne 25$.

1)  Rút gọn biểu thức $P$

2) Tìm các giá trị của $x$ để $P = \dfrac{5}{7}$

Câu II (2,0 điểm):

1. Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $\left( d \right)$ có phương trình $y = \left( {2m + 1} \right)x + m$ ($m$ là tham số). Tìm $m$ để đường thẳng $\left( d \right)$ đi qua điểm $A\left( {1;5} \right)$.

2. Giải hệ phương trình $\left\{ \begin{array}{l}4x + 3y = 11\\4x - y = 7\end{array} \right.$.

Câu III (2,0 điểm):

1. Giải phương trình ${x^2} - 6x + 5 = 0$.

2. Cho phương trình ${x^2} - 2x + m - 1 = 0$ (m là tham số). Tìm các giá trị của m để phương trình có hai nghiệm ${x_1},\,{x_2}$ thỏa mãn hệ thức ${x_1}^4 - {x_1}^3 = {x_2}^4 - {x_2}^3.$

Câu IV (3,0 điểm):

Cho tam giác nhọn ABC nội tiếp đường tròn $(O)$. Các đường cao AD, BE, CF (D thuộc B, E thuộc AC, F thuộc AB) của tam giác cắt nhau tại H, M là trung điểm của cạnh BC.

1. Chứng minh AEHF là tứ giác nội tiếp

2. Chứng minh các đường thẳng ME và MF là các tiếp tuyến của đường tròn ngoại tiếp tứ giác AEHF.

3. Chứng minh $DE + DF \le BC$.

Câu V (1,0 điểm):

Cho ba số thực $x,\,\,y,\,\,z$ thay đổi thỏa mãn các điều kiện $x > \dfrac{1}{4},\,\,y > \dfrac{1}{3},\,\,z > \dfrac{1}{2}$ và $\dfrac{4}{{4x + 3}} + \dfrac{3}{{3y + 2}} + \dfrac{2}{{2z + 1}} \ge 2$. Tìm giá trị lớn nhất của biểu thức $Q = \left( {4x - 1} \right)\left( {3y - 1} \right)\left( {2z - 1} \right)$. 

Lời giải chi tiết

Câu I (2,0 điểm):

Phương pháp:

1) Vận dụng hẳng đẳng thức $a - b = \left( {\sqrt a  - \sqrt b } \right)\left( {\sqrt a  + \sqrt b } \right)$ xác định mẫu thức chung của biểu thức $P$

Thực hiện các phép toán với các phân thức đại số để rút bọn biểu thức ban đầu.

2) Quy đồng phân thức, giải phương trình tìm được nghiệm đối chiếu điều kiện và kết luận.

Cách giải:

1) Với $x \ge 0,\,\,x \ne 25$ ta có:

$\begin{array}{l}P = \dfrac{{\sqrt x }}{{\sqrt x  + 5}} + \dfrac{{2\sqrt x }}{{\sqrt x  - 5}} - \dfrac{{3x + 25}}{{x - 25}}\\\,\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x  - 5} \right) + 2\sqrt x \left( {\sqrt x  + 5} \right) - 3x - 25}}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}}\\\,\,\,\,\, = \dfrac{{x - 5\sqrt x  + 2x + 10\sqrt x  - 3x - 25}}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}}\\\,\,\,\,\, = \dfrac{{5\sqrt x  - 25}}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}} = \dfrac{{5\left( {\sqrt x  - 5} \right)}}{{\left( {\sqrt x  + 5} \right)\left( {\sqrt x  - 5} \right)}} = \dfrac{5}{{\sqrt x  + 5}}\end{array}$

Vậy $P = \dfrac{5}{{\sqrt x  + 5}}$ với $x \ge 0,\,\,x \ne 25$.

2) Ta có: $P = \dfrac{5}{{\sqrt x  + 5}}$ với $x \ge 0,\,\,x \ne 25$

$\begin{array}{l}P = \dfrac{5}{7} \Leftrightarrow \dfrac{5}{{\sqrt x  + 5}} = \dfrac{5}{7}\\ \Leftrightarrow \sqrt x  + 5 = 7 \Leftrightarrow \sqrt x  = 2 \Leftrightarrow x = 4\,\,\left( {tm} \right)\end{array}$

Vậy $x = 4$ thỏa mãn yêu cầu bài toán.

Câu II (2,0 điểm)

Phương pháp:

1) Thay tọa độ điểm $A\left( {1;5} \right)$ vào đường thẳng $\left( d \right)$, tìm được tham số $m$.

2) Vận dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình.

Cách giải:

1) Vì $A\left( {1;5} \right) \in d$ nên thay tọa độ điểm $A$ vào phương trình đường thẳng $\left( d \right)$ ta có:

$5 = \left( {2m + 1} \right).1 + m \Leftrightarrow 3m + 1 = 5 \Leftrightarrow m = \dfrac{4}{3}$.

Vậy $m = \dfrac{4}{3}$.

2) Ta có: $\left\{ \begin{array}{l}4x + 3y = 11\\4x - y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4y = 4\\4x - y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\4x - 1 = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 2\end{array} \right.$

Vậy nghiệm của hệ phương trình là $\left( {x;y} \right) = \left( {2;1} \right)$.

Câu III (2,0 điểm):

Phương pháp:

1) Vận dụng công thức nghiệm của phương trình bậc hai một ẩn số xác định được nghiệm của phương trình.

2) Phương trình đã cho có nghiệm $\Leftrightarrow \Delta ' \ge 0$.

Áp dụng hệ thức Vi – ét, tính được ${x_1} + {x_2};{x_1}.{x_2}$

Biến đổi biểu thức ban đầu của đề bài để xuất hiện ${x_1} + {x_2};{x_1}.{x_2}$, thay tham số $m$ vào để giải và tìm tham số $m$.

Cách giải:

1) Ta có: $\Delta  = {\left( { - 6} \right)^2} - 4.1.5 = 16 > 0$ nên phương trình có 2 nghiệm phân biệt: $\left[ \begin{array}{l}{x_1} = \dfrac{{6 + \sqrt {16} }}{2} = 5\\{x_2} = \dfrac{{6 - \sqrt {16} }}{2} = 1\end{array} \right.$

Vậy phương trình có tập nghiệm $S = \left\{ {1;\,\,5} \right\}$.

2) Phương trình ${x^2} - 2x + m - 1 = 0$ có $\Delta ' = 1 - m + 1 = 2 - m$.

Phương trình đã cho có nghiệm $\Leftrightarrow \Delta ' \ge 0 \Leftrightarrow 2 - m \ge 0 \Leftrightarrow m \le 2$.

Khi đó theo định lí Vi-ét ta có: $\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}.{x_2} = m - 1}\end{array}} \right.\,\,\left( 1 \right)$

Do ${x_1},\,\,\,{x_2}$ là nghiệm của phương trình ${x^2} - 2x + m - 1 = 0$ nên ta có: $\left\{ \begin{array}{l}{x_1}^2 = 2{x_1} - m + 1\\{x_2}^2 = 2{x_2} - m + 1\end{array} \right.$

Theo bài ra ta có:

 $\begin{array}{l}\,\,\,\,\,\,\,{x_1}^4 - {x_1}^3 = {x_2}^4 - {x_2}^3\\ \Leftrightarrow {x_1}^4 - {x_2}^4 - \left( {{x_1}^3 - {x_2}^3} \right) = 0\\ \Leftrightarrow \left( {{x_1}^2 + {x_2}^2} \right)\left( {{x_1}^2 - {x_2}^2} \right) - \left( {{x_1} - {x_2}} \right)\left( {{x_1}^2 + {x_1}{x_2} + {x_2}^2} \right) = 0\\ \Rightarrow \left( {2\left( {{x_1} + {x_2}} \right) - 2m + 2} \right)\left( {2{x_1} - m + 1 - 2{x_2} + m - 1} \right) - \left( {{x_1} - {x_2}} \right)\left[ {2\left( {{x_1} + {x_2}} \right) - 2m + 2 + m - 1} \right]\\ \Leftrightarrow \left[ {2.2 - 2m + 2} \right].2\left( {{x_1} - {x_2}} \right) - \left( {{x_1} - {x_2}} \right)\left[ {2.2 - m + 1} \right]\\ \Leftrightarrow \left( {{x_1} - {x_2}} \right)\left[ {2\left( {6 - 2m} \right) - 5 + m} \right] = 0\\ \Leftrightarrow \left( {{x_1} - {x_2}} \right)\left( {3m + 7} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x_1} = {x_2}}\\{m = \dfrac{7}{3}\,\,\,\left( {ktm} \right)}\end{array}} \right.\end{array}$

Thay ${x_1} = {x_2}$ vào (1) ta được: $\left\{ {\begin{array}{*{20}{c}}{2{x_1} = 2}\\{{x_1}^2 = m - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_1} = 1}\\{m = 2\,\,\,\left( {tm} \right)}\end{array}} \right.$

Vậy $m = 2.$

Câu IV (3,0 điểm):

Phương pháp:

1) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp: Tứ giác có tổng hai góc đối bằng ${180^0}$ là tứ giác nội tiếp.

2) Gọi I là trung điểm của AH suy ra I là tâm đường tròn ngoại tiếp tứ giác AEHF.

Chứng minh $\angle MFI = {90^0}$ hay $IF \bot MF$, do đó $MF$ là tiếp tuyến của đường tròn ngoại tiếp tứ giác $AEHF$

Chứng minh tương tự ta được $ME$ là tiếp tuyến của đường tròn ngoại tiếp tứ giác $AEHF$.

Cách giải:

1) Xét tứ giác AEHF có: $\angle AFH + \angle AEH = {90^0} + {90^0} = {180^0}$

Mà hai góc này đối diện nhau trong tứ giác $AEHF$ nên tứ giác $AEHF$ là tứ giác nội tiếp đường tròn tâm $M$ đường kính $BC$ (dhnb).

2) Gọi I là trung điểm của AH suy ra I là tâm đường tròn ngoại tiếp tứ giác AEHF.

$\Rightarrow IH = IF$ $\Rightarrow \Delta H$ cân tại I $\Rightarrow \angle IFH = \angle IHF$ (tính chất tam giác cân).

Mà $\angle IHF = \angle DHC$ (đối đỉnh) $\Rightarrow \angle IFH = \angle DHC$   (1)

Do $\Delta BFC$ vuông tại F, M là trung điểm của BC nên $MF = \dfrac{1}{2}BC = MC$ (định lí đường trung tuyến trong tam giác vuông) $\Rightarrow \Delta MFC$ cân tại $M$ $\Rightarrow \angle MFH = \angle MCF$    (2)

Cộng (1) với (2) ta được: $\angle MFH + \angle IFH = \angle DHC + \angle MCF = {90^0}$ (Do tam giác $CDH$ vuông tại $D$).

Suy ra: $\angle MFI = {90^0}$ hay $IF \bot MF$.

Vậy $MF$ là tiếp tuyến của đường tròn ngoại tiếp tứ giác $AEHF$.

Chứng minh tương tự ta được $ME$ là tiếp tuyến của đường tròn ngoại tiếp tứ giác $AEHF$.

3) Giả sử $DE + DF \le BC \Leftrightarrow \left( {DE + DF} \right).BC \le B{C^2} \Leftrightarrow DE.BC + DF.BC \le B{C^2}$.

Chứng minh $B{C^2} = BF.BA + CE.CA$

Chứng minh $DF.BC = AC.BF$ và $DE.BC = AB.CE$, cộng từng vế của hai đẳng thức chứng minh được $\left( {CE - BF} \right)\left( {AC - AB} \right) \ge 0\,\,\,\left( * \right)$

Biện luận, từ đó có điều phải chứng minh.

3) Giả sử $DE + DF \le BC \Leftrightarrow \left( {DE + DF} \right).BC \le B{C^2} \Leftrightarrow DE.BC + DF.BC \le B{C^2}$.

Dễ dàng chứng minh được các tứ giác $ACDF,\,\,ABDE$ là các tứ giác nội tiếp nên ta có:

$\begin{array}{l}B{C^2} = \left( {BD + CD} \right).BC\\\,\,\,\,\,\,\,\,\,\, = BD.BC + CB.CD\\\,\,\,\,\,\,\,\,\,\, = BF.BA + CE.CA\end{array}$

Xét $\Delta BDF$ và $\Delta BAC$ có:

$\angle ABC$ chung;

$\angle BFD = \angle BCA$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp $ACDF$)

$\Rightarrow \Delta BDF \sim \Delta BAC\,\,\left( {g.g} \right)$

$\Rightarrow \dfrac{{DF}}{{AC}} = \dfrac{{BF}}{{BC}} \Rightarrow DF.BC = AC.BF$  (1)

Chứng minh tương tự ta có $\Delta CDE \sim \Delta CAB\,\,\left( {g.g} \right)$ $\Rightarrow \dfrac{{DE}}{{AB}} = \dfrac{{CE}}{{BC}} \Rightarrow DE.BC = AB.CE$  (2)

Cộng vế theo vế của (1) và (2) ta có:

$\begin{array}{l}DF.BC + DE.BC = AC.BF + AB.CE\\ \Rightarrow \left( {DE + DF} \right).BC = AC.BF + AB.CE\end{array}$

Vì $\left( {DE + DF} \right).BC \le B{C^2}$

$\begin{array}{l} \Rightarrow AC.BF + AB.CE \le BF.BA + CE.CA\\ \Rightarrow BF.BA + CE.CA - AC.BF - AB.CE \ge 0\\ \Leftrightarrow AC\left( {CE - BF} \right) + AB\left( {BF - CE} \right) \ge 0\\ \Leftrightarrow \left( {CE - BF} \right)\left( {AC - AB} \right) \ge 0\,\,\,\left( * \right)\end{array}$

Không mất tính tổng quát, ta giả sử $AC \ge AB$, khi đó ta cần chứng minh $CE - BF \ge 0 \Leftrightarrow CE \ge BF$.

Áp dụng định lí Pytago ta có: $\left\{ \begin{array}{l}C{E^2} = B{C^2} - B{E^2}\\B{F^2} = B{C^2} - C{F^2}\end{array} \right.$.

Mà $\left\{ \begin{array}{l}2{S_{\Delta ABC}} = BE.AC = CF.AB\\AB \le AC\end{array} \right. \Leftrightarrow BE \le CF$ .

$\Rightarrow C{E^2} \ge B{F^2} \Rightarrow CE \ge BF$ $\Rightarrow \left( * \right)$ đúng nên giả sử ban đầu là đúng.

Vậy $DE + DF \le BC$.

Câu V (1,0 điểm):

Phương pháp:

Áp dụng bất đẳng thức Cô – si, chứng minh được:$\dfrac{4}{{4x + 3}} \ge 2\sqrt {\dfrac{{3y - 1}}{{3y + 2}}.\dfrac{{2z - 1}}{{2z + 1}}}$;$\dfrac{3}{{3y + 2}} \ge 2\sqrt {\dfrac{{4x - 1}}{{4x + 3}}.\dfrac{{2z - 1}}{{2z + 1}}}$; $\dfrac{2}{{2z + 1}} \ge 2\sqrt {\dfrac{{4x - 1}}{{4x + 3}}.\dfrac{{3y - 1}}{{3y + 2}}}$

Nhân vế theo vế 3 BĐT trên ta được điều phải chứng minh.

Cách giải:

Ta có:

$\begin{array}{l}\,\,\,\,\,\,\dfrac{4}{{4x + 3}} + \dfrac{3}{{3y + 2}} + \dfrac{2}{{2z + 1}} \ge 2\\ \Leftrightarrow \dfrac{4}{{4x + 3}} \ge \left( {1 - \dfrac{3}{{3y + 2}}} \right) + \left( {1 - \dfrac{2}{{2z + 1}}} \right)\\ \Leftrightarrow \dfrac{4}{{4x + 3}} \ge \dfrac{{3y - 1}}{{3y + 2}} + \dfrac{{2z - 1}}{{2z + 1}}\\ \Leftrightarrow \dfrac{4}{{4x + 3}} \ge 2\sqrt {\dfrac{{3y - 1}}{{3y + 2}}.\dfrac{{2z - 1}}{{2z + 1}}} \,\,\left( {BDT\,\,Co - si} \right)\end{array}$

Chứng minh tương tự ta có:

$\dfrac{3}{{3y + 2}} \ge 2\sqrt {\dfrac{{4x - 1}}{{4x + 3}}.\dfrac{{2z - 1}}{{2z + 1}}} ;\,\,\dfrac{2}{{2z + 1}} \ge 2\sqrt {\dfrac{{4x - 1}}{{4x + 3}}.\dfrac{{3y - 1}}{{3y + 2}}}$

Nhân vế theo vế 3 BĐT trên ta được:

$\begin{array}{l}\dfrac{4}{{4x + 3}}.\dfrac{3}{{3y + 2}}.\dfrac{2}{{2z + 1}} \ge 2\sqrt {\dfrac{{3y - 1}}{{3y + 2}}.\dfrac{{2z - 1}}{{2z + 1}}} .2\sqrt {\dfrac{{4x - 1}}{{4x + 3}}.\dfrac{{2z - 1}}{{2z + 1}}} .2\sqrt {\dfrac{{4x - 1}}{{4x + 3}}.\dfrac{{3y - 1}}{{3y + 2}}} \\ \Leftrightarrow \dfrac{4}{{4x + 3}}.\dfrac{3}{{3y + 2}}.\dfrac{2}{{2z + 1}} \ge 8\dfrac{{4x - 1}}{{4x + 3}}.\dfrac{{3y - 1}}{{3y + 2}}.\dfrac{{2z - 1}}{{2z + 1}}\\ \Leftrightarrow 24 \ge 8Q \Leftrightarrow Q \le 3\end{array}$

Vậy ${Q_{\max }} = 3$. Dấu “=” xảy ra $\Leftrightarrow \left( {x;y;z} \right) = \left( {\dfrac{3}{4};\dfrac{5}{6};1} \right)$.