Đề thi vào 10 môn Toán Tiền Giang năm 2023

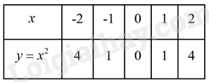
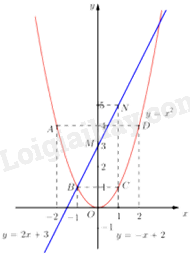
Đề bài

Câu 1:

1. Tính giá trị của biểu thức $A = \sqrt {27} {\rm{ \;}} - \frac{3}{{\sqrt 3 }} - \sqrt 3$.

2. Giải các phương trình và hệ phương trình sau:

a) ${x^2} + 3x - 10 = 0$;

b) ${x^4} - 8{x^2} - 9 = 0$;

c) $\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array}} \right.$

Câu 2: Trong mặt phẳng tọa độ Oxy, cho parabol $\left( P \right):y = {x^2}$ và đường thẳng $\left( d \right):y = 2x + 3$.

1. Vẽ parabol $\left( P \right)$ và đường thẳng $\left( d \right)$ trên cùng một mặt phẳng tọa độ.

2. Bằng phép tính, tìm tọa độ các giao điểm của $\left( P \right)$ và $\left( d \right)$.

Câu 3: 

1. Gọi ${x_1}$ và ${x_2}$ là hai nghiệm của phương trình ${x^2} + x - 10 = 0$. Không giải phương trình, tính giá trị của biểu thức $A = x_1^2 + x_2^2 - 3{x_1}{x_2}$

2. Tìm tất cả các giá trị của tham số $m$ để phương trình ${x^2} + \left( {m + 1} \right)x + \frac{1}{4}{m^2} + 1 = 0$ có hai nghiệm phân biệt.

Câu 4: Một khu vườn hình chữ nhật có diện tích bằng $150\;{{\rm{m}}^2}$. Hơi khu vườn có chiều dài và chiều rộng bằng bao nhiêu mét, biết rằng chiều dài lơn hơn chiều rộng $5\;{\rm{m}}$ ?

Câu 5: Cho nửa đường tròn tâm $O$ đường kính AB. Trên nửa đường tròn đó lấy điểm $C(C$ khác $A$ và $B$ ), kẻ CH vuông góc với AB tại $H$. Gọi $K$ là điểm nằm giữa $C$ và $H$, tia AK cắt đường tròn tại điểm thứ hai là $D$.

1. Chứng minh BHKD là một tứ giác nội tiếp.

2. Chứng minh tam giác ACK đồng dạng với tam giác ADC và chứng minh $AK \cdot AD = A{C^2}$.

Câu 6: Một hình trụ có bán kính đáy bằng $4\;{\rm{cm}}$, chiều cao bằng $12\;{\rm{cm}}$. Tính diện tích xung quanh và thể tích của hình trụ đã cho.

----- HẾT -----

Lời giải chi tiết

Câu 1 (TH):

Phương pháp:

1. Khai căn và tính giá trị biểu thức.

2. a) Tính $\Delta$ và giải phương trình

b) Đặt $t = {x^2}$

c) Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

1.

$\begin{array}{*{20}{r}}{A = \sqrt {27} {\rm{\;}} - \frac{3}{{\sqrt 3 }} - \sqrt 3 }&{}\\{A = \sqrt {{3^2} \cdot 3} {\rm{\;}} - \frac{{{{(\sqrt 3 )}^2}}}{{\sqrt 3 }} - \sqrt 3 }&{}\\{A = 3\sqrt 3 {\rm{\;}} - \sqrt 3 {\rm{\;}} - \sqrt 3 }&{}\\{A = \left( {3 - 1 - 1} \right)\sqrt 3 }&{}\\{A = \sqrt 3 }&{}\end{array}$

Vậy $A = \sqrt 3$.

2. Giải các phương trình và hệ phương trình sau:

a) ${x^2} + 3x - 10 = 0$

Ta có: $\Delta  = {3^2} - 4 \cdot 1 \cdot \left( { - 10} \right) = 49 > 0$ nên phương trình có 2 nghiệm phân biệt

$\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - 3 + \sqrt {49} }}{{2.1}} = 2}\\{{x_2} = \frac{{ - 3 - \sqrt {49} }}{{2.1}} = {\rm{ \;}} - 5}\end{array}} \right.$

Vậy tập nghiệm của phương trình là $S = \left\{ {2; - 5} \right\}$.

b) ${x^4} - 8{x^2} - 9 = 0$.

Đặt $t = {x^2} \ge 0$, phương trình trở thành ${t^2} - 8t - 9 = 0$.

Ta có $a - b + c = 1 - \left( { - 8} \right) + \left( { - 9} \right) = 0$ nên phương trình có 2 nghiệm phân biệt

Với $t = 9 \Rightarrow {x^2} = 9 \Leftrightarrow x = {\rm{ \;}} \pm 3$.

Vạy tập nghiệm của phương trình là $S = \left\{ { \pm 3} \right\}$.

c) $\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array}} \right.$

$\left\{ {\begin{array}{*{20}{l}}{3x + y = 2}\\{x - y = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x = 8}\\{y = x - 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = {\rm{ \;}} - 4}\end{array}} \right.} \right.} \right.$

Vậy hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( {2; - 4} \right)$

Câu 2 (TH):

Phương pháp:

a) Tìm 2 điểm để vẽ đường thẳng d và 5 điểm để vẽ parabol P.

b) Xét phương trình hoành độ giao điểm và tìm 2 nghiệm của phương trình đó.

Cách giải:

a) Vẽ parabol $\left( P \right)$ và đường thẳng $\left( d \right)$ trên cùng một mặt phẳng tọa độ.

Vẽ đường thẳng $\left( d \right)$ :

Với $x = 0$ thì $y = 2.0 + 3 = 3$

Với $x = 1$ thì $y = 2.1 + 3 = 5$

$\Rightarrow$ Đồ thị hàm số $y = 2x + 3$ là đường thẳng đi qua $M\left( {0;3} \right)$ và $N\left( {1;5} \right)$

Vẽ parabol $\left( P \right)$ :

Ta có bảng giá trị sau:

$\Rightarrow$ Đồ thị hàm số là đường cong parabol đi qua các điểm $O\left( {0;0} \right);A\left( { - 2;4} \right);B\left( { - 1;1} \right);C\left( {1;1} \right);D\left( {2;4} \right)$

Hệ số $a = 1 > 0$ nên parabol có bể cong hướng lên. Đồ thị hàm số nhận ${\rm{Oy}}$ làm trục đối xứng.

Ta vẽ được đồ thị hàm số $y = {x^2}$ như sau:

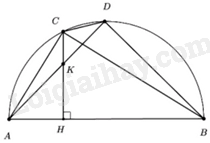
b) Bằng phép tính, tìm tọa độ các giao điểm $\left( d \right)$ và $\left( P \right)$.

Xét phương trình hoành độ giao điểm của $\left( d \right)$ và $\left( P \right)$ ta có:

${x^2} = 2x + 3 \Leftrightarrow {x^2} - 2x - 3 = 0$

Ta có: $a - b + c = 1 - \left( { - 2} \right) + \left( { - 3} \right) = 0$ nên phương trình có 2 nghiệm phân biệt $\left[ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 1}\\{x = {\rm{ \;}} - \frac{c}{a} = 3}\end{array}} \right.$.

Với $x = {\rm{ \;}} - 1$ thì $y = {( - 1)^2} = 1$

Với $x = 3$ thì $y = {3^2} = 9$

Vậy $\left( P \right)$ cắt $\left( d \right)$ tại 2 điểm có tọa độ là: $\left( { - 1;1} \right)$ và $\left( {3;9} \right)$.

Câu 3 (VD):

Phương pháp:

1. Áp dụng hệ thức vi-et $\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.$

2. Phương trình có hai nghiệm phân biệt khi $\Delta {\rm{ \;}} > 0$

Cách giải:

1. Do ${x_1},{x_2}$ là hai nghiệm của phương trình ${x^2} + x - 10 = 0$ nên áp dụng hệ thức Vi-et ta có $\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = {\rm{ \;}} - 1}\\{{x_1}{x_2} = {\rm{ \;}} - 10}\end{array}} \right.$

Ta có $A = x_1^2 + x_2^2 - 3{x_1}{x_2}$

$\begin{array}{*{20}{r}}{ = x_1^2 + 2{x_1}{x_2} + x_2^2 - 5{x_1}{x_2}}&\;\\{ = {{\left( {{x_1} + {x_2}} \right)}^2} - 5{x_1}{x_2}}&\;\\{ = {{( - 1)}^2} - 5\left( { - 10} \right)}&\;\\{ = 51}&\;\end{array}$

Vây $A = 51$.

2. Ta có $\Delta  = {(m + 1)^2} - 4 \cdot 1 \cdot \left( {\frac{1}{4}{m^2} + 1} \right) = {m^2} + 2m + 1 - {m^2} - 4 = 2m - 3$

Để phương trình có 2 nghiệm phân biệt thì $\Delta  > 0 \Leftrightarrow 2m - 3 > 0 \Leftrightarrow m > \frac{3}{2}$

Vậy $m > \frac{3}{2}$ thì phương trình có 2 nghiệm phân biệt .

Câu 4 (TH):

Phương pháp:

- Gọi chiều dài hình chữ nhật là x, khi đó chiều rộng là x – 5.

- Ta tìm được phương trình là: Chiều dài nhân với chiều rộng bằng 150.

Cách giải:

Gọi chiều dài hình chữ nhật là $x(x > 5$, mét)

Do chiều dài lớn hơn chiều rộng $5\;{\rm{m}}$ nên chiều rộng hình chữ nhật là $x - 5\left( {\;{\rm{m}}} \right)$

Diện tích hình chữ nhật là $x\left( {x - 5} \right)\left( {{{\rm{m}}^2}} \right)$

Do diện tích khu vườn bằng $150\;{{\rm{m}}^2}$ nên ta có phương trình

$\begin{array}{*{20}{r}}{}&{x\left( {x - 5} \right) = 150}\\{}&{{x^2} - 5x - 150 = 0}\end{array}$

Ta có $\Delta  = {( - 5)^2} - 4 \cdot 1 \cdot \left( { - 150} \right) = 625 > 0$ nên phương trình có 2 nghiệm phân biệt

$\left[ {\begin{array}{*{20}{l}}{{x_1} = \frac{{ - \left( { - 5} \right) + \sqrt {625} }}{2} = 15\left( {{\rm{tm}}} \right)}\\{{x_2} = \frac{{ - \left( { - 5} \right) - \sqrt {625} }}{2} = {\rm{ \;}} - 10\left( {{\rm{ktm}}} \right)}\end{array}} \right.$

Vậy chiều dài hình chữ nhật là $15\;{\rm{m}}$, chiều rộng hình chữ nhật là $10\;{\rm{m}}$.

Câu 5 (VD):

Phương pháp:

1. Tứ giác có tổng hai góc đối bằng $180^\circ$ là tứ giác nội tiếp.

2. Chứng minh  từ đó suy ra điều phải chứng minh.

Cách giải:

1. Do $CH \bot AB\left( {gt} \right) \Rightarrow \angle KHB = 90^\circ$

Ta có $\angle ADB = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \angle KHB + \angle KDB = 90^\circ  + 90^\circ  = 180^\circ$

Mà hai góc này ở vị trí đối diện nên tứ giác HKDB nội tiếp (dhnb) (đpcm)

2. Ta có $\angle ACB = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \angle ACH + \angle HCB = 90^\circ$

Mà $\angle HCB + \angle HBC = 90^\circ$ (do  vuông tại ${\rm{H}}$ )

$\Rightarrow \angle ACH = \angle ABC$ (cùng phụ $\angle HCB)$

Mà $\angle ABC = \angle ADC$ (góc nội tiếp cùng chắn cung ${\rm{AC}}$ )

$\Rightarrow \angle ACH = \angle CDA\;{\rm{hay}}\;\angle ACK = \angle CDA$

Xét $\Delta ACK$ và $\Delta ADC$ có:

$\angle ACK = \angle CDA$

$\angle CAD$ chung

$\Rightarrow \Delta ACK\backsim \Delta ADC$ (g.g)

$\Rightarrow \frac{{AC}}{{AD}} = \frac{{AK}}{{AC}} \Leftrightarrow A{C^2} = AD \cdot AK$ (đpcm)

Câu 6 (TH):

Phương pháp:

Áp dụng công thức:

${S_{{\rm{sq}}}} = 2\pi rh$

$V = \pi {r^2}h$

Cách giải:

Diện tích xung quanh của hình trụ là:

${S_{{\rm{sq}}}} = 2\pi rh = 2\pi {\rm{ \;}} \cdot 4 \cdot 12 = 96\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)$

Thể tích của hình trụ là:

$V = \pi {r^2}h = \pi {\rm{ \;}} \cdot {4^2} \cdot 12 = 192\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)$

Vậy diện tích xung quanh của hình trụ là $96\pi {\rm{c}}{{\rm{m}}^2}$, thể tích hình trụ là: $192\pi {\rm{c}}{{\rm{m}}^3}$.

-----HẾT-----