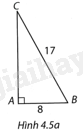
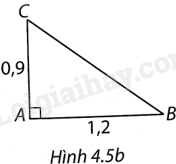
Giải bài 1 trang 73 vở thực hành Toán 9Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc nhọn B và C khi biết: a) (AB = 8cm,BC = 17cm); b) (AC = 0,9cm,AB = 1,2cm). Đề bài Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc nhọn B và C khi biết: a) \(AB = 8cm,BC = 17cm\); b) \(AC = 0,9cm,AB = 1,2cm\). Phương pháp giải - Xem chi tiết - Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có + Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \). + Tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \). + Tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \). + Tỉ số giữa cạnh kề và cạnh đối gọi là cot của \(\alpha \). - Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia. Lời giải chi tiết a) (H.4.5a) Theo định lí Pythagore, ta có \(A{C^2} + A{B^2} = B{C^2}\) \(A{C^2} = B{C^2} - A{B^2}\) \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{17}^2} - {8^2}} = 15\left( {cm} \right)\) Từ đó \(\sin B = \cos C = \frac{{AC}}{{BC}} = \frac{{15}}{{17}};\\\cos B = \sin C = \frac{{AB}}{{BC}} = \frac{8}{{17}};\\\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{{15}}{8};\\\cot B = \tan C = \frac{{AB}}{{AC}} = \frac{8}{{15}}\) b) (H.4.5b) Theo Pythagore, ta có \(BC = \sqrt {A{C^2} + A{B^2}} = \sqrt {{{1,2}^2} + {{0,9}^2}} = 1,5\) Từ đó \(\sin B = \cos C = \frac{{AC}}{{BC}} = \frac{{0,9}}{{1,5}} = \frac{3}{5},\\\cos B = \sin C = \frac{{AB}}{{BC}} = \frac{{1,2}}{{1,5}} = \frac{4}{5}, \\\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{{0,9}}{{1,2}} = \frac{3}{4},\\\cot B = \tan C = \frac{{AB}}{{AC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}.\)
|