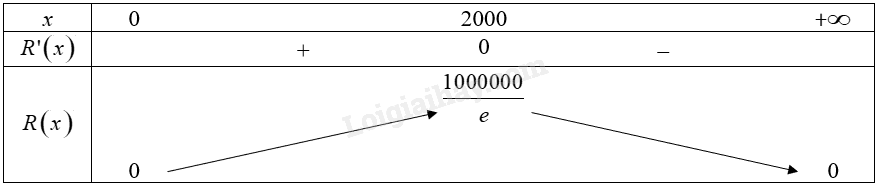
Giải bài 12 trang 23 Chuyên đề học tập Toán 12 - Chân trời sáng tạoTheo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là (p) nghìn đồng thì sẽ có ({rm{x}}) người mua vé xem biểu diễn, giữa (p) và ({rm{x}}) có mối liên hệ: (p = 500.{e^{ - 0,0005x}}). Đơn vị tổ chức nên bán vé với giá bao nhiêu thì đạt được doanh thu (tổng số tiền bán vé) cao nhất? Đề bài Theo kết quả thăm dò trước một buổi biểu diễn văn nghệ ngoài trời, nếu giá bán mỗi vé là \(p\) nghìn đồng thì sẽ có \({\rm{x}}\) người mua vé xem biểu diễn, giữa \(p\) và \({\rm{x}}\) có mối liên hệ: \(p = 500.{e^{ - 0,0005x}}\). Đơn vị tổ chức nên bán vé với giá bao nhiêu thì đạt được doanh thu (tổng số tiền bán vé) cao nhất? Phương pháp giải - Xem chi tiết • Biểu thị doanh thu thông qua \(p\) và \({\rm{x}}\). • Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm: ‒ Lập bảng biến thiên của hàm số trên tập hợp đó. ‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số. Lời giải chi tiết Doanh thu khi công ty bán được \(x\) vé với mỗi vé là \(p\) nghìn đồng là: \(R\left( x \right) = p.x = 500.{e^{ - 0,0005x}}.x\) (triệu đồng) Xét hàm số \(R\left( x \right) = 500.{e^{ - 0,0005x}}.x\) trên khoảng \(\left( {0; + \infty } \right)\). Ta có: \(\begin{array}{l}R'\left( x \right) = {\left( {500.{e^{ - 0,0005x}}} \right)^\prime }.x + 500.{e^{ - 0,0005x}}.{\left( x \right)^\prime } = 500.\left( { - 0,0005} \right).{e^{ - 0,0005x}}.x + 500.{e^{ - 0,0005x}}\\ = 500.{e^{ - 0,0005x}}\left( {1 - 0,0005x} \right)\end{array}\) \(R'\left( x \right) = 0 \Leftrightarrow 500.{e^{ - 0,0005x}}\left( {1 - 0,0005x} \right) = 0 \Leftrightarrow x = 2000\). Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left( {0; + \infty } \right)} R\left( x \right) = R\left( {2000} \right) = \frac{{1000000}}{e}\). Vậy đơn vị tổ chức nên bán vé với giá \(p = 500.{e^{ - 0,0005.2000}} = \frac{{500}}{e} \approx 184\) nghìn đồng thì đạt được doanh thu (tổng số tiền bán vé) cao nhất.
|