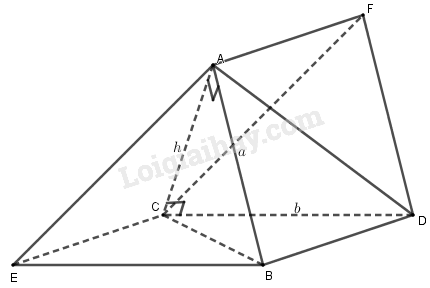
Bài 1.32 trang 20 SBT hình học 12Giải bài 1.32 trang 20 sách bài tập hình học 12. Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, các mặt (SAB) và (SAD) vuông góc với đáy. Góc giữa mặt (SAC) và đáy bằng 60, AB = 2a , BC = a. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SC theo a. Đề bài Cho hai đoạn thẳng \(AB\) và \(CD\) chéo nhau, \(AC\) là đường vuông góc chung của chúng. Biết rằng \(AC = h, AB = a, CD = b\) và góc giữa hai đường thẳng \(AB\) và \(CD\) bằng \({60^0}\). Hãy tính thể tích của khối tứ diện \(ABCD\). Phương pháp giải - Xem chi tiết - Dựng hình hình bình hành \(CDBE\) và \(ABDF\). - Tính thể tích tứ diện \(ABCE\) rồi suy ra thể tích khối tứ diện \(ABCD\). Lời giải chi tiết
Dựng hình hình bình hành \(CDBE\) và \(ABDF\). Khi đó, \(ABE.FDC\) là hình lăng trụ. Ta có: \(AC \bot CD,CD//BE\) \( \Rightarrow AC \bot BE\), mà \(AC \bot AB\) nên \(AC \bot \left( {ABE} \right)\). Lại có \(\widehat {\left( {AB,CD} \right)} = \widehat {\left( {AB,BE} \right)}\) \( = \widehat {ABE} = {60^0}\) \( \Rightarrow {S_{ABE}} = \dfrac{1}{2}AB.BE.\sin \widehat {ABE}\)\( = \dfrac{1}{2}ab.\sin {60^0} = \dfrac{{ab\sqrt 3 }}{4}\) \( \Rightarrow {V_{C.ABE}} = \dfrac{1}{3}{S_{ABE}}.AC\)\( = \dfrac{1}{3}.\dfrac{{ab\sqrt 3 }}{4}.h = \dfrac{{abh\sqrt 3 }}{{12}}\) Từ đó suy ra \({V_{A.BCD}} = {V_{A.BCE}} = \dfrac{{abh\sqrt 3 }}{{12}}\). HocTot.XYZ
|