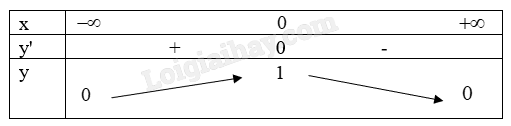
Giải bài 1.56 trang 34 sách bài tập toán 12 - Kết nối tri thứcCho hàm số (y = {e^{ - frac{{{x^2}}}{2}}}) có đồ thị (left( C right)). Xét các mệnh đề sau: (I): Điểm cực đại của đồ thị (left( C right)) là (left( {0;1} right)). (II): Trục hoành là tiệm cận ngang của đồ thị (left( C right)). (III): Giá trị lớn nhất của hàm số là 1. (IV): Điểm cực đại của đồ thị (left( C right)) là (x = 0). Số mệnh đề đúng trong các mệnh đề trên là A. (4). B. (1). C. (2). D. (3). Đề bài Cho hàm số \(y = {e^{ - \frac{{{x^2}}}{2}}}\) có đồ thị \(\left( C \right)\). Xét các mệnh đề sau: (I): Điểm cực đại của đồ thị \(\left( C \right)\) là \(\left( {0;1} \right)\). (II): Trục hoành là tiệm cận ngang của đồ thị \(\left( C \right)\). (III): Giá trị lớn nhất của hàm số là 1. (IV): Điểm cực đại của đồ thị \(\left( C \right)\) là \(x = 0\). Số mệnh đề đúng trong các mệnh đề trên là A. \(4\) B. \(1\) C. \(2\) D. \(3\) Phương pháp giải - Xem chi tiết Xét từng mệnh đề, tìm cực đại, tiệm cận, giá trị lớn nhất để biết được mệnh đề đó đúng hay sai. Lời giải chi tiết Ta có \(y' = \left( {\frac{{ - {x^2}}}{2}} \right)'{e^{\frac{{ - {x^2}}}{2}}} = - x{e^{\frac{{ - {x^2}}}{2}}} = - x\frac{1}{{{e^{\frac{{{x^2}}}{2}}}}} = \frac{{ - x}}{{{e^{\frac{{{x^2}}}{2}}}}}\). Suy ra \(y' = 0 \Leftrightarrow \frac{{ - x}}{{{e^{\frac{{{x^2}}}{2}}}}} = 0 \Leftrightarrow x = 0\). Ta xét dấu của đạo hàm. Qua điểm \(x = 0\), đạo hàm thay đổi giá trị từ dương sang âm. Do đó \(x = 0\) là một điểm cực đại của hàm số.
Xét lần lượt các mệnh đề ta có: + Mệnh đề (I): Do \(x = 0\) là một điểm cực đại của hàm số nên điểm cực đại của đồ thị hàm số là \(\left( {0;1} \right)\). Suy ra (I) đúng. + Mệnh đề (II): Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {e^{ - \frac{{{x^2}}}{2}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{e^{\frac{{{x^2}}}{2}}}}} = 0\) suy ra \(y = 0\) hay \(Ox\) là tiệm cận ngang của \(\left( C \right)\). Suy ra (II) đúng. + Mệnh đề (III): Giá trị lớn nhất của hàm số là 1. Suy ra (III) đúng. + Mệnh đề (IV): Theo mệnh đề (I) đúng ta có điểm cực đại của đồ thị hàm số là \(\left( {0;1} \right)\) chứ không phải là \(x = 0\) nên (IV) sai. Vậy có tất cả 3 mệnh đề đúng nên ta chọn đáp án D.
|