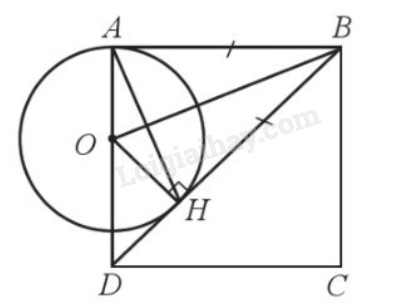
Giải bài 16 trang 106 sách bài tập toán 9 - Cánh diều tập 1Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O. a) So sánh OA, OH, HD. b) Xác định vị trí tương đối của BD và đường tròn (O; OA). Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho hình vuông ABCD. Trên đường chéo BD, lấy điểm H sao cho BH = AB. Qua điểm H kẻ đường thẳng vuông góc với BD cắt AD tại O. a) So sánh OA, OH, HD. b) Xác định vị trí tương đối của BD và đường tròn (O; OA). Phương pháp giải - Xem chi tiết a) Bước 1: Chứng minh ΔOAB=ΔOHB để suy ra OA=OH Bước 2: Chứng minh tam giác ODH là tam giác vuông cân để suy ra OH=DH. b) Chỉ ra BD là tiếp tuyến của (O). Lời giải chi tiết
a) Do ABCD là hình vuông nên ^DAB=^ADC=90∘, và DB là tia phân giác của góc ADB nên ^ADB=45∘. Xét tam giác OAB và tam giác OHB có: ^OAB=^OHB=90∘; OB chung; AB=BH Suy ra ΔOAB=ΔOHB (cạnh huyền – cạnh góc vuông) Do đó OA=OH (cặp cạnh tương ứng) (1) Xét tam giác ODH vuông tại H có ^ODH=45∘ nên tam giác ODH là tam giác vuông cân tại H, do đó OH=DH (2) Từ (1) và (2) ta có OA=OH=DH. b) Vì OA=OH và OH vuông góc với Bd tại H nên BD là tiếp tuyến của (O). Vậy BD tiếp xúc với (O;OA).  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
