Bài 1.64 trang 37 SBT giải tích 12Giải bài 1.64 trang 37 sách bài tập giải tích 12. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1)...
Lựa chọn câu để xem lời giải nhanh hơn
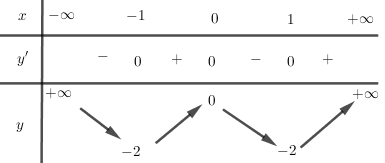
Cho hàm số \(y = 2{x^4} - 4{x^2}\)(1) LG câu a Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1). Phương pháp giải: - Tìm TXĐ. - Xét sự biến thiên. - Vẽ đồ thị hàm số. Giải chi tiết: Tập xác định : \(D = R\) \(y' = 8{x^3} - 8x = 8x({x^2} - 1)\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 1\end{array} \right.\) Hàm số đồng biến trên mỗi khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\) Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\) Hàm số đạt cực đại tại \(x = 0;{y_{CD}} = 0\) Hàm số đạt cực tiểu tại \(x = \pm 1;{y_{CT}} = - 2\) Giới hạn: \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \) \(y'' = 24{x^2} - 8;\)\(y'' = 0 \Leftrightarrow {x^2} = \dfrac{1}{3} \Leftrightarrow x = \pm \dfrac{{\sqrt 3 }}{3}\) Đồ thị có hai điểm uốn: \({I_1}\left( { - \dfrac{{\sqrt 3 }}{3}; - \dfrac{{10}}{9}} \right);\)\({I_2}\left( {\dfrac{{\sqrt 3 }}{3}; - \dfrac{{10}}{9}} \right)\). Bảng biến thiên:
Đồ thị:
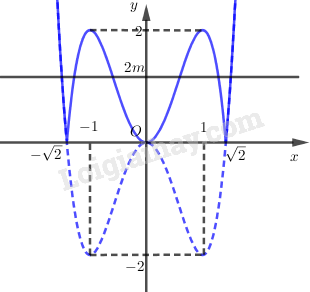
Đồ thị cắt trục hoành tại: \(A( - \sqrt 2 ;0),O(0;0),B(\sqrt 2 ;0)\). LG b Với giá trị nào của \(m\), phương trình \({x^2}|{x^2} - 2| = m\) có đúng \(6\) nghiệm thực phân biệt? (Đề thi đại học năm 2009; khối B) Phương pháp giải: - Biến đổi phương trình đã cho về \(\left| {2{x^4} - 4{x^2}} \right| = 2m\). - Dựng đồ thị hàm số \(y = \left| {2{x^4} - 4{x^2}} \right|\) từ đồ thị hàm số đã vẽ ở ý a: + Giữ nguyên phần đồ thị phía trên trục \(Ox\). + Lấy đối xứng phần dưới qua \(Ox\) và xóa phần dưới đi. - Biện luận số nghiệm dựa vào số giao điểm của đường thẳng \(y = 2m\) và đồ thị vừa vẽ được. Giải chi tiết: Ta có: \({x^2}|{x^2} - 2| = m\)\( \Leftrightarrow 2{x^2}\left| {{x^2} - 2} \right| = 2m\)\( \Leftrightarrow \left| {2{x^2}\left( {{x^2} - 2} \right)} \right| = 2m\)\( \Leftrightarrow \left| {2{x^4} - 4{x^2}} \right| = 2m\) Từ đồ thị hàm số \(y = 2{x^4}-4{x^2}\) có thể suy ra đồ thị của hàm số \(y = \left| {2{x^4} - 4{x^2}} \right|\) như sau:
Phương trình : \(\left| {2{x^4} - 4{x^2}} \right| = 2m\) có \(6\) nghiệm phân biệt khi và chỉ khi đường thẳng \(y = 2m\) giao với đồ thị trên tại \(6\) điểm phân biệt \( \Leftrightarrow 0 < 2m < 2\) \( \Leftrightarrow 0 < m < 1\). Vậy \(0 < m < 1\). HocTot.XYZ
|