Bài 1.77 trang 40 SBT giải tích 12Giải bài 1.77 trang 40 sách bài tập giải tích 12. Xác định a để hàm số luôn luôn đồng biến...
Lựa chọn câu để xem lời giải nhanh hơn
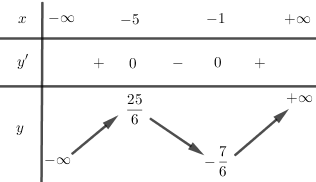
Cho hàm số \(y = \dfrac{{(a - 1){x^3}}}{3} + a{x^2} + (3a - 2)x\). LG a Xác định \(a\) để hàm số luôn luôn đồng biến. Phương pháp giải: - Xét trường hợp \(a = 1\), kiểm tra xem hàm số có luôn đồng biến hay không. - Trường hợp \(a \ne 1\), hàm số luôn đồng biến trên \(\mathbb{R}\) nếu \(y' \ge 0\) với mọi \(x \in \mathbb{R}\). Lời giải chi tiết: Ta có: \(y' = (a - 1){x^2} + 2ax + 3a - 2\). +) Với \(a = 1,y' = 2x + 1\;\) đổi dấu khi \(x\) đi qua \( - \dfrac{1}{2}\). Hàm số không luôn luôn đồng biến. +) Với \(a \ne 1\) thì với mọi \(x\) mà tại đó \(y' \ge 0\)\( \Leftrightarrow \left\{ \begin{array}{l}a - 1 > 0\\\Delta ' \le 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \begin{array}{l}a > 1\\\left[ \begin{array}{l}a \ge 2\\a \le \dfrac{1}{2}\end{array} \right.\end{array} \right.\) \( \Leftrightarrow a \ge 2\) (khi \(a = 2\) thì \(y' = 0\;\) chỉ tại \(x = - 2\)) Vậy với \(a \ge 2\) hàm số luôn luôn đồng biến. LG b Xác định \(a\) để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt. Phương pháp giải: - Xét phương trình hoành độ giao điểm của đồ thị hàm số với đường thẳng \(y = 0\). - Tìm điều kiện để phương trình đó có ba nghiệm phân biệt và kết luận. Lời giải chi tiết: Đồ thị cắt trục hoành tại ba điểm phân biệt khi và chỉ khi phương trình \(y = 0\) có ba nghiệm phân biệt. Ta có: \(y = 0\)\(\Leftrightarrow \dfrac{{(a - 1){x^3}}}{3} + a{x^2} + (3a - 2)x=0\) \( \Leftrightarrow x\left[ {\dfrac{{(a - 1){x^2}}}{3} + ax + 3a - 2} \right] = 0\) \( \Leftrightarrow x\left[ {(a - 1){x^2} + 3ax + 9a - 6} \right] = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\\left( {a - 1} \right){x^2} + 3ax + 9a - 6 = 0\,\left( * \right)\end{array} \right.\) \(y = 0\) có ba nghiệm phân biệt khi và chỉ khi phương trình \(\left( * \right)\) có hai nghiệm phân biệt khác \(0\). \( \Leftrightarrow \left\{ \begin{array}{l}a - 1 \ne 0\\\Delta > 0\\9a-6 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a - 1 \ne 0\\9{a^2} - 4(a - 1)(9a - 6) > 0\\9a - 6 \ne 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 1\\\dfrac{{10 - 2\sqrt 7 }}{9} < a < \dfrac{{10 + 2\sqrt 7 }}{9}\\a \ne \dfrac{2}{3}\end{array} \right.\) Vậy \(a \in \left( {\dfrac{{10 - 2\sqrt 7 }}{9};\dfrac{{10 + 2\sqrt 7 }}{9}} \right)\backslash \left\{ {1;\dfrac{2}{3}} \right\}\). LG c Khảo sát sự biến thiên và vẽ đồ thị \(\left( C \right)\) của hàm số ứng với \(a = \dfrac{3}{2}\). Từ đó suy ra đồ thị của hàm số: \(y = \left| {\dfrac{{{x^3}}}{6} + \dfrac{{3{x^2}}}{2} + \dfrac{{5x}}{2}} \right|\) Phương pháp giải: - Thay \(a = \dfrac{3}{2}\) vào được hàm số cần khảo sát. - Khảo sát tóm tắt: + Tìm TXĐ. + Xét chiều biến thiên. + Vẽ đồ thị. - Dựng đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) từ đồ thị hàm số \(y = f\left( x \right)\): + Giữ nguyên phần đồ thị phía trên trục hoành. + Lấy đối xứng phần dưới qua trục hoành và xóa phần dưới cũ đi. Lời giải chi tiết: Khi \(a = \dfrac{3}{2}\) thì \(y = \dfrac{{{x^3}}}{6} + \dfrac{{3{x^2}}}{2} + \dfrac{{5x}}{2}\) Ta có: \(y' = \dfrac{{{x^2}}}{2} + 3x + \dfrac{5}{2}\);\(y' = 0 \Leftrightarrow {x^2} + 6x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 5\end{array} \right.\) Bảng biến thiên:
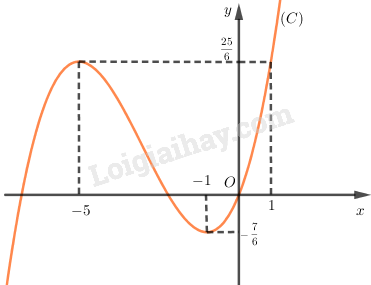
Đồ thị:
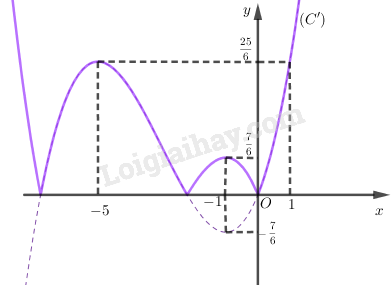
Ta có: \(y =\left| {\dfrac{{{x^3}}}{6} + \dfrac{{3{x^2}}}{2} + \dfrac{{5x}}{2}} \right|\) \(= \left\{ \begin{array}{l} Từ đồ thị hàm số \(y = \dfrac{{{x^3}}}{6} + \dfrac{{3{x^2}}}{2} + \dfrac{{5x}}{2}\) ta suy ra ngay đồ thị hàm số \(y = \left| {\dfrac{{{x^3}}}{6} + \dfrac{{3{x^2}}}{2} + \dfrac{{5x}}{2}} \right|\) như sau:
HocTot.XYZ
|