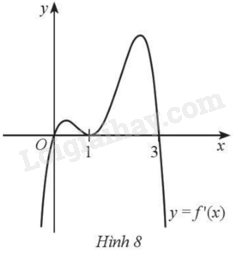
Giải bài 18 trang 13 sách bài tập toán 12 - Cánh diềuTrong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 8. a) \(f'\left( x \right) = 0\) khi \(x = 0,x = 1,x = 3\). b) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\). c) \(f'\left( x \right) > 0\) khi \(x \in \left( {0;3} \right)\). d) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0;3} \right)\). Đề bài Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 8. a) \(f'\left( x \right) = 0\) khi \(x = 0,x = 1,x = 3\). b) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\). c) \(f'\left( x \right) > 0\) khi \(x \in \left( {0;3} \right)\). d) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0;3} \right)\).
Phương pháp giải - Xem chi tiết Dựa vào đồ thị hàm số \(y = f'\left( x \right)\), lập bảng xét dấu đạo hàm của hàm số \(y = f\left( x \right)\), từ đó xác định số điểm cực trị của hàm số \(y = f\left( x \right)\). Lời giải chi tiết Do hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) nên hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\). Căn cứ vào đồ thị hàm số \(y = f'\left( x \right)\), ta có: \(f'\left( x \right) = 0\) khi \(x = 0,x = 1,x = 3\). Vậy a) đúng. Dựa vào vị trí của đồ thị hàm số \(y = f'\left( x \right)\) so với trục hoành, ta có bảng xét dấu \(f'\left( x \right)\) như sau:
Vì hàm số xác định trên \(\mathbb{R}\) nên hàm số đồng biến trên các khoảng \(\left( {0;1} \right)\) và \(\left( {1;3} \right)\) hay hàm số đồng biến trên khoảng \(\left( {0;3} \right)\). Vậy b) sai, d) đúng. Khi \(x \in \left( {0;3} \right)\), ta có \(f'\left( x \right) > 0,\forall x \ne 1\) và \(f\left( 1 \right) = 0\). Vậy c) sai. a) Đ. b) S. c) S. d) Đ.
|