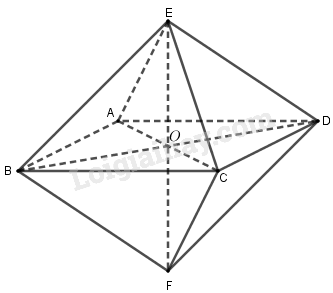
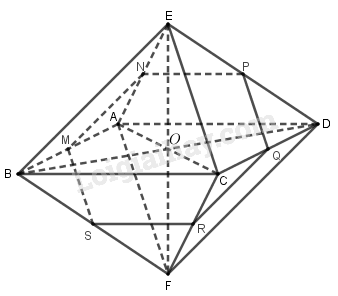
Bài 1.9 trang 12 SBT hình học 12Giải bài 1.9 trang 12 sách bài tập hình học 12. Cho khối bát diện đều ABCDEF (hình vẽ). Gọi O là giao điểm của AC và BD, M và N theo thứ tự là trung điểm của AB và AE. Tính diện tích thiết diện tạo bởi khối bát diện đó và mặt phẳng (OMN). Đề bài Cho khối bát diện đều \(ABCDEF\) (hình vẽ). Gọi \(O\) là giao điểm của \(AC\) và \(BD, M\) và \(N\) theo thứ tự là trung điểm của \(AB\) và \(AE\). Tính diện tích thiết diện tạo bởi khối bát diện đó và mặt phẳng \((OMN)\).
Phương pháp giải - Xem chi tiết Dựng thiết diện của bát hiện đều khi cắt bởi \(\left( {OMN} \right)\). Sử dụng mối quan hệ song song của đường thẳng và mặt phẳng. Lời giải chi tiết
Ta có khối bát diện đều \(ABCDEF\), cạnh \(a\). Do \(MN//\left( {DEBF} \right)\) nên giao của mặt phẳng \(\left( {OMN} \right)\) với mặt phẳng \(\left( {DEBF} \right)\) là đường thẳng qua \(O\) và song song với \(MN\). Trong \(\left( {DEBF} \right)\), qua \(O\) kẻ đường thẳng \(PS//MN\) \(\left( {P \in DE,S \in BF} \right)\). Do \(\left( {ADE} \right)//\left( {BCF} \right)\) nên \(\left( {OMN} \right)\) cắt \(\left( {BCF} \right)\) theo giao tuyến qua \(S\) và song song với \(NP\) cắt \(FC\) tại trung điểm \(R\). Tương tự, \(\left( {OMN} \right)\) cắt \(DC\) tại trung điểm \(Q\) của\(DC\). Suy ra thiết diện tạo bởi hình bát diện đã cho với mặt phẳng \(\left( {OMN} \right)\) là lục giác đều có cạnh bằng \(\dfrac{a}{2}\). Do đó diện tích thiết diện là: \(S = 6{S_{\Delta OMN}} = 6.{\left( {\dfrac{a}{2}} \right)^2}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{3\sqrt 3 }}{8}{a^2}\). HocTot.XYZ
|