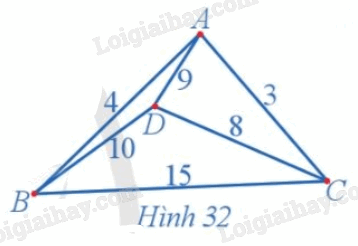
Giải bài 2 trang 49 Chuyên đề học tập Toán 11 Cánh diềuCó bốn địa điểm với độ dài quãng đường giữa các địa điểm (đơn vị: kilômét) mô tả trong Hình 32. Đề bài Có bốn địa điểm với độ dài quãng đường giữa các địa điểm (đơn vị: kilômét) mô tả trong Hình 32. Sử dụng thuật toán láng giềng gần nhất, tìm các chu trình xuất phát từ một đỉnh đi qua tất cả các địa điểm, mỗi địa điểm đúng một lần sao cho tổng độ dài các cạnh của chu trình là nhỏ nhất.
Phương pháp giải - Xem chi tiết Bước 1. Chọn một đỉnh bắt đầu, ta gọi là đỉnh V. Bước 2. Xuất phát từ đỉnh hiện hành, chọn cạnh có độ dài nhỏ nhất nối đến một trong các đỉnh chưa đến. Đánh dấu đỉnh cuối của cạnh vừa chọn. Bước 3. Xuất phát từ đỉnh vừa đánh dấu, nếu còn đỉnh chưa đến thì quay lại bước 2. Bước 4. Quay lại đỉnh V. Lời giải chi tiết Dễ thấy đồ thị Hình 32 có chu trình Hamilton. +) Sử dụng thuật toán láng giềng gần nhất đối với đỉnh xuất phát A, ta có: Từ A, đỉnh gần nhất là C, AC = 3 km; Từ C, đỉnh chưa đến gần nhất là D, CD = 8 km; Từ D, đỉnh chưa đến gần nhất là B, DB = 10 km; Đến đây không còn đỉnh chưa đến, vì vậy quay về A, BA = 4 km. Tổng quãng đường theo chu trình ACDBA là: 3 + 8 + 10 + 4 = 25 (km). Tương tự bắt đầu với những đỉnh khác, ta có bảng sau:
Các chu trình trên thỏa mãn điều kiện xuất phát từ một đỉnh đi qua tất cả các địa điểm, mỗi địa điểm đúng một lần và tổng độ dài các cạnh của chu trình là nhỏ nhất.
|