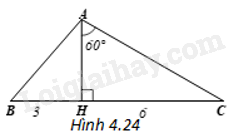
Giải bài 2 trang 85 vở thực hành Toán 9Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết (HB = 3cm,HC = 6cm,widehat {HAC} = {60^o}). Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ). Đề bài Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết \(HB = 3cm,HC = 6cm,\widehat {HAC} = {60^o}\). Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ). Phương pháp giải - Xem chi tiết + Tam giác vuông AHC có: \(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\) nên tính được AC; \(AH = HC.\cot \widehat {HAC}\) nên tính được AH. + \(\widehat {ACB} = {90^o} - \widehat {HAC} = {30^o}\) + Áp dụng định lí Pythagore trong tam giác vuông AHB tính được AB. + \(\tan B = \frac{{AH}}{{BH}}\) từ đó tính được góc B. + Trong tam giác ABC, ta có: \(\widehat {BAC} = {180^o} - \widehat C - \widehat B\), từ đó tính được góc BAC. Lời giải chi tiết (H.4.24)
Tam giác ACH vuông tại H, \(HC = 6cm,\widehat {HAC} = {60^o}\). Trong tam giác vuông AHC, ta có \(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\) nên \(AC = \frac{{HC}}{{\sin \widehat {HAC}}} = \frac{6}{{\sin {{60}^o}}} = 4\sqrt 3 \approx 7\left( {cm} \right)\) \(AH = HC.\cot \widehat {HAC} = 6.\cot {60^o} = 2\sqrt 3 \left( {cm} \right)\) \(\widehat {ACB}\) là góc phụ với \(\widehat {HAC}\) nên \(\widehat {ACB} = {90^o} - \widehat {HAC} = {30^o}\) Trong tam giác vuông AHB, ta có \(A{B^2} = A{H^2} + H{B^2} = {3^2} + {\left( {2\sqrt 3 } \right)^2} = 21\) nên \(AB = \sqrt {21} \approx 5\left( {cm} \right)\) \(\tan B = \frac{{AH}}{{BH}} = \frac{{2\sqrt 3 }}{3}\) nên \(\widehat B \approx {49^o}\) Trong tam giác ABC, ta có \(\widehat {BAC} = {180^o} - \widehat C - \widehat B = {180^o} - {30^o} - {49^o} \approx {101^o}\)
|