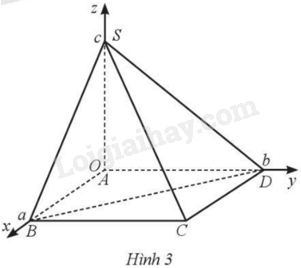
Giải bài 20 trang 48 sách bài tập toán 12 - Cánh diềuTrong không gian với hệ toạ độ (Oxyz), cho hình chóp (S.ABCD) có đáy là hình chữ nhật và các điểm (Aleft( {0;0;0} right),Bleft( {a;0;0} right),Dleft( {0;b;0} right),Sleft( {0;0;c} right)) với (a,b,c) là các số dương (Hình 3). a) Tìm toạ độ của điểm (C), trung điểm (M) của (BC), trọng tâm (G) của tam giác (SCD). b) Lập phương trình mặt phẳng (left( {SBD} right)). c) Tính khoảng cách từ điểm (G) đến mặt phẳng (left( {SBD} right)). Đề bài Trong không gian với hệ toạ độ \(Oxyz\), cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật và các điểm \(A\left( {0;0;0} \right),B\left( {a;0;0} \right),D\left( {0;b;0} \right),S\left( {0;0;c} \right)\) với \(a,b,c\) là các số dương (Hình 3). a) Tìm toạ độ của điểm \(C\), trung điểm \(M\) của \(BC\), trọng tâm \(G\) của tam giác \(SCD\). b) Lập phương trình mặt phẳng \(\left( {SBD} \right)\). c) Tính khoảng cách từ điểm \(G\) đến mặt phẳng \(\left( {SBD} \right)\).
Phương pháp giải - Xem chi tiết ‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\). ‒ Sử dụng công thức toạ độ trung điểm \(M\) của đoạn thẳng \(AB\): \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{y_A} + {z_B}}}{2}} \right)\). ‒ Sử dụng công thức toạ độ trọng tâm \(G\) của tam giác \(ABC\): \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\). ‒ Phương trình mặt phẳng theo đoạn chắn: Mặt phẳng đi qua ba điểm \(A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right)\) với \(abc \ne 0\) có phương trình là \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\). ‒ Khoảng cách từ điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + C{\rm{z}} + D = 0\): \(d\left( {{M_0};\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{{\rm{z}}_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\). Lời giải chi tiết a) Giả sử \(C\left( {{x_C};{y_C};{z_C}} \right)\). \(\overrightarrow {AB} = \left( {a;0;0} \right),\overrightarrow {DC} = \left( {{x_C};{y_C} - b;{z_C}} \right)\). Tứ giác \(ABCD\) là hình chữ nhật khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \). \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}a = {x_C}\\0 = {y_C} - b\\0 = {z_C}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = a\\{y_C} = b\\{z_C} = 0\end{array} \right.\). Vậy \(C\left( {a;b;0} \right)\). \(M\) là trung điểm của \(BC\) nên ta có: \(M\left( {\frac{{a + a}}{2};\frac{{0 + b}}{2};\frac{{0 + 0}}{2}} \right)\) hay \(M\left( {a;\frac{b}{2};0} \right)\). \(G\) là trọng tâm của tam giác \(SCD\) nên ta có: \(G\left( {\frac{{0 + a + 0}}{3};\frac{{0 + b + b}}{3};\frac{{c + 0 + 0}}{3}} \right)\) hay \(G\left( {\frac{a}{3};\frac{{2b}}{3};\frac{c}{3}} \right)\). b) Phương trình mặt phẳng \(\left( {SBD} \right)\) là: \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) hay \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} - 1 = 0\). c) Khoảng cách từ điểm \(G\) đến mặt phẳng \(\left( {SBD} \right)\) bằng: \(\begin{array}{l}d\left( {G,\left( {SBD} \right)} \right) = \frac{{\left| {\frac{{\frac{a}{3}}}{a} + \frac{{\frac{{2b}}{3}}}{b} + \frac{{\frac{c}{3}}}{c} - 1} \right|}}{{\sqrt {{{\left( {\frac{1}{a}} \right)}^2} + {{\left( {\frac{1}{b}} \right)}^2} + {{\left( {\frac{1}{c}} \right)}^2}} }} = \frac{1}{{3\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} }}\\ = \frac{1}{{3\sqrt {\frac{{{b^2}{c^2} + {a^2}{c^2} + {a^2}{b^2}}}{{{a^2}{b^2}{c^2}}}} }} = \frac{{abc}}{{3\sqrt {{a^2}{b^2} + {a^2}{c^2} + {b^2}{c^2}} }}\end{array}\)
|