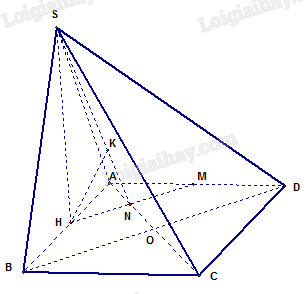
Giải bài 20 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sốngCho hình chóp (S.ABCD) có mặt phẳng (left( {SAB} right)) vuông góc với mặt đáy (left( {ABCD} right)) Đề bài Cho hình chóp \(S.ABCD\) có mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy \(\left( {ABCD} \right)\), tam giác \(SAB\) đều, đáy \(ABCD\) là hình vuông cạnh bằng \(a\). Gọi \(H\) là trung điểm của cạnh \(AB\). Khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAC} \right)\) bằng A. \(\frac{{a\sqrt {30} }}{5}\). B. \(\frac{{a\sqrt {30} }}{{10}}\). C. \(\frac{{a\sqrt 6 }}{{10}}\). D. \(\frac{{a\sqrt 6 }}{5}\). Phương pháp giải - Xem chi tiết Chứng minh \(SH \bot \left( {ABCD} \right)\), tính \(SH\). Dựng hình chiếu \(K\) của \(H\) trên \(\left( {SAC} \right)\). Tính \(HK\). Lời giải chi tiết
Ta có \(AC \bot BD;AC = a\sqrt 2 \); Gọi \(M\) là trung điểm của \(AD\) và \(HM \cap AC = N\). Do \(\Delta SAB\) là tam giác đều nên \(SH \bot AB;SH = \frac{{a\sqrt 3 }}{2}\). Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right) \Rightarrow SH \bot AC\); \(HM\) là đường trung bình tam giác \(ABD \Rightarrow HM//BD \Rightarrow HM \bot AC\). \(HN = \frac{1}{2}HM = \frac{1}{4}AC = \frac{{a\sqrt 2 }}{4}\). Vì \(SH \bot AC;HN \bot AC \Rightarrow \left( {SHN} \right) \bot AC\). Kẻ \(HK \bot SN\) tại \(K\). Ta chứng minh được \(HK \bot SN;AC \Rightarrow HK \bot \left( {SAC} \right)\) tại \(K\). Suy ra: \(d\left( {H,\left( {SAC} \right)} \right) = HK\). Ta có: \(HK = \frac{{HS.HN}}{{\sqrt {H{S^2} + H{N^2}} }}\) \( = \frac{{\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 2 }}{4}}}{{\sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{4}} \right)}^2}} }}\)\( = \frac{{a\sqrt {21} }}{{14}}\). Chọn C
|