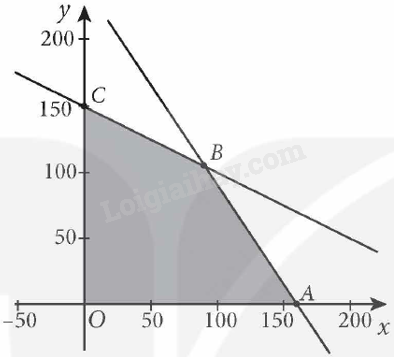
Giải bài 2.11 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thứcMột cửa hàng chuyên về cà phê, có sẵn 75 kg cà phê Colombia nguyên chất và 120 kg cà phê thương hiệu của cửa hàng. Những thứ này sẽ được pha thành các gói cà phê 1 kg như sau: Một gói tiêu chuẩn có chứa 250g cà phê Colombia nguyên chất và 750g cà phê thương hiệu, một gói cao cấp chứa 500g cà phê Colombia nguyên chất và 500g cà phê thương hiệu. a) Gọi x là số gói cà phê tiêu chuẩn và y là số gói cà phê cao cấp, hãy viết hệ bất phương trình bậc nhất mô tả số lượng gói có thể có của mỗi loại. b Đề bài Một cửa hàng chuyên về cà phê, có sẵn 75 kg cà phê Colombia nguyên chất và 120 kg cà phê thương hiệu của cửa hàng. Những thứ này sẽ được pha thành các gói cà phê 1 kg như sau: Một gói tiêu chuẩn có chứa 250g cà phê Colombia nguyên chất và 750g cà phê thương hiệu, một gói cao cấp chứa 500g cà phê Colombia nguyên chất và 500g cà phê thương hiệu. a) Gọi x là số gói cà phê tiêu chuẩn và y là số gói cà phê cao cấp, hãy viết hệ bất phương trình bậc nhất mô tả số lượng gói có thể có của mỗi loại. b) Biểu diễn hình học miền nghiệm của hệ bất phương trình bậc nhất nhận được ở cầu a và tìm các đỉnh của miền nghiệm. c) Lợi nhuận của mỗi gói cà phê tiêu chuẩn là 30 nghìn đồng và của mỗi gói cà phê cao cấp là 40 nghìn đồng. Hỏi cần chuẩn bị bao nhiêu gói cà phê mỗi loại để lợi nhuận thu được là lớn nhất? Giả sử rằng tất cả các gói cà phê đã chuẩn bị đều có thể bán được. Phương pháp giải - Xem chi tiết F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các điểm cực biên. Lời giải chi tiết a)Theo bài ra, ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\250x + 500y \le 75{\rm{ }}000\\750x + 500y \le 120{\rm{ }}000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0,y \ge 0\\x + 2y \le 300\\3x + 2y \le 480\end{array} \right.\) b) Miền nghiệm của hệ bất phương trình trên là tứ giác OABC được tô màu như hình vẽ dưới đây:
Điểm cực biên: \(O(0;0),A(160;0),B(90;105),C(0;150).\) c) Lợi nhuận thu được là \(F(x,y) = 30x + 40y\) (nghìn đồng) Ta có: \(F(0;0) = 0,F(160,0) = 4800;F(90;105) = 6900;F(0;150) = 6000\) Vậy lợi nhuận thu được lớn nhất là 6 900 nghìn đồng (6 triệu 900 nghìn đồng) khi x=90 và y=105 tức là cần chuẩn bị 90 gói cà phê tiêu chuẩn và 105 gói cà phê cao cấp.
|