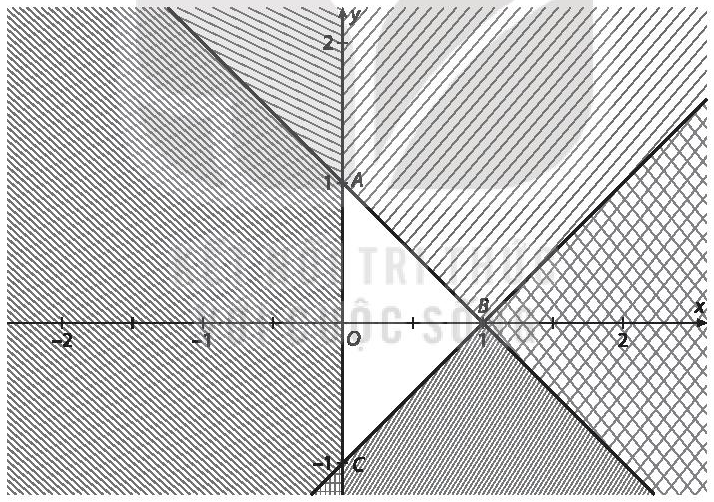
Giải bài 2.17 trang 25 sách bài tập toán 10 - Kết nối tri thức với cuộc sốngMiền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác ABC (miền không bị gạch) ? Đề bài Miền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác \(ABC\) (miền không bị gạch)? A. \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \ge 1}\\{x \ge 0}\end{array}.} \right.\) B. \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \le 1}\\{x \ge 0}\end{array}} \right..\) C. \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 1}\\{x + y \ge - 1}\\{x \ge 0}\end{array}.} \right.\) D. \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge - 1}\\{x + y \ge - 1}\\{y \ge 0}\end{array}.} \right.\) Lời giải chi tiết Dễ thấy đáp án D sai. Thay điểm \(O\left( {0;0} \right)\) vào bất phương trình, \(x - y \ge 1\)ta được: \(0 - 0 = 0 > 1\) (vô lý) \( \Rightarrow \) loại đáp án A. Thay điểm \(O\left( {0;0} \right)\) vào bất phương trình, \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 1}\\{x - y \le 1}\\{x \ge 0}\end{array}} \right.\) ta được: \(\left\{ {\begin{array}{*{20}{c}}{0 + 0 = 0 < 1}\\{0 - 0 < 1}\\{0 \ge 0}\end{array}} \right.\) (thỏa mãn) \( \Rightarrow \) đáp án B đúng. Chọn B.
|