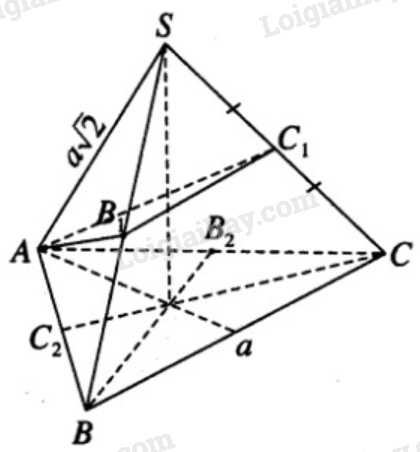
Bài 2.18 trang 61 SBT hình học 12Giải bài 2.18 trang 61 SBT hình học 12. Hình chóp S.ABC là hình chóp tam giác đều , có cạnh đáy bằng a và cạnh bên bằng. Một mặt cầu đi qua đỉnh A và tiếp xúc với hai cạnh SB , SC tại trung điểm của mỗi cạnh. Đề bài Hình chóp S.ABC là hình chóp tam giác đều, có cạnh đáy bằng a và cạnh bên bằng \(a\sqrt 2 \) . Một mặt cầu đi qua đỉnh A và tiếp xúc với hai cạnh SB , SC tại trung điểm của mỗi cạnh. a) Chứng minh rằng mặt cầu đó đi qua trung điểm của AB và AC. b) Gọi giao điểm thứ hai của mặt cầu với đường thẳng SA là D. Tính độ dài của AD và SD. Phương pháp giải - Xem chi tiết a) Gọi \(B_2,C_2\) là giao điểm của mặt cầu với các cạnh \(AC,AB\). Chứng minh \(B_2,C_2\) là các trung điểm bằng cách tính độ dài \(BC_2\) và \(CB_2\). b) Sử dụng hệ thức \(SD.SA = SB_1^2\). Lời giải chi tiết
a) Giả sử mặt cầu đi qua đỉnh A của hình chóp và tiếp xúc với cạnh SB tại B1, tiếp xúc với cạnh SC tại C1. Khi đó mặt cầu cắt cạnh AB, AC lần lượt tại các điểm C2, B2. Mặt phẳng (SAB) cắt mặt cầu đó theo giao tuyến là một đường tròn. Đường tròn này tiếp xúc với SB tại B1 và đi qua A và C2. Do đó, ta có: BB12 = BA. BC2 trong đó \(B{B_1} = {{SB} \over 2} = {{a\sqrt 2 } \over 2}\). Do đó, \(B{B_1}^2 = {{{a^2}} \over 2}\) Vậy \({{{a^2}} \over 2} = a.B{C_2} \Rightarrow B{C_2} = {{{a^2}} \over 2}:a = {a \over 2}\) Điều đó chứng tỏ mặt cầu nói trên đi qua trung điểm C2 của đoạn AB. Lí luận tương tự ta chứng minh được mặt cầu đó đi qua trung điểm B2 của AC. b) Gọi giao điểm thứ hai của mặt cầu với đường thẳng SA là D, ta có: \(S{\rm{D}}{\rm{.SA = SB}}_1^2\) hay \(SD.a\sqrt 2 = {({{a\sqrt 2 } \over 2})^2} = {{{a^2}} \over 2}\) Do đó, \(SD = {{{a^2}} \over 2}:a\sqrt 2 = {{a\sqrt 2 } \over 4}\) và \(AD = SA - SD = {{3a\sqrt 2 } \over 4}\) HocTot.XYZ
|