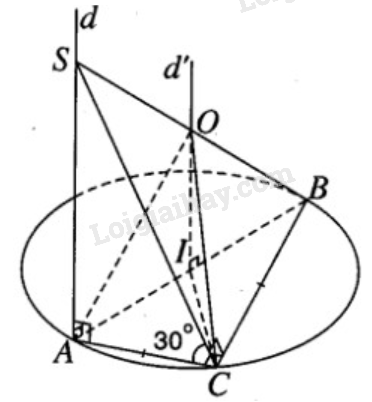
Bài 2.29 trang 63 SBT hình học 12Giải bài 2.29 trang 63 sách bài tập hình học 12. Cho tam giác vuông cân ABC có cạnh huyền AB = 2a. Trên đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC), lấy một điểm S khác A, ta được tứ diện SABC. Đề bài Cho tam giác vuông cân ABC có cạnh huyền AB = 2a. Trên đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC), lấy một điểm S khác A, ta được tứ diện SABC. a) Xác định tâm mặt cầu ngoại tiếp tứ diện SABC. b) Tính bán kính của mặt cầu ngoại tiếp tứ diện SABC trong trường hợp mặt phẳng (SBC) tạo với mặt phẳng (ABC) một góc bằng 300. Phương pháp giải - Xem chi tiết a) Tâm của mặt cầu ngoại tiếp tứ diện các đều các đỉnh. b) Tính toán dựa vào các kiến thức hình học đã biết. Lời giải chi tiết
a) Gọi I là trung điểm của cạnh AB. Vì tam giác ABC vuông cân tại C nên ta có IA = IB = IC. Vậy I là tâm đường tròn ngoại tiếp tam giác ABC. Do đó, tâm mặt cầu ngoại tiếp tứ diện SABC phải nằm trên đường thẳng d’ vuông góc với mặt phẳng (ABC) tại I. Ta suy ra d’ // d. Do đó d’ cắt SB tại trung điểm O của đoạn SB. Ta có OB = OS = OA = OC và như vậy O là tâm đường tròn ngoại tiếp tứ diện SABC. b) Trường hợp mặt phẳng (SBC) tạo với mặt phẳng (ABC) một góc 300 thì góc của hai mặt phẳng đó chính là góc \(\widehat {SCA}\). Thật vậy, vì \(SA \bot (ABC)\) mà \(AC \bot CB\) nên ta có \(SC \bot CB\). Do đó \(\widehat {SCA} = {30^0}\) . Vì AB = 2a nên ta có \(AC = a\sqrt 2 \) ta suy ra \(SA = AC.\tan {30^0} = a\sqrt 2 .{{\sqrt 3 } \over 3} = {{a\sqrt 6 } \over 3}\). Gọi r là bán kính mặt cầu ngoại tiếp tứ diện khi \(\widehat {SCA} = {30^0}\) . Ta có \(r = {{SB} \over 2} = OA = OB = OC = {\rm{OS}}\), trong đó SB2 = SA2 + AB2 Vậy \(S{B^2} = {{6{a^2}} \over 9} + 4{a^2} = {{42{a^2}} \over 9}\). Do đó, \(SB = {{a\sqrt {42} } \over 3}\) Ta suy ra \(r = {{SB} \over 2} = {{a\sqrt {42} } \over 6}\). HocTot.XYZ
|