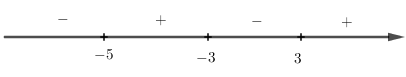Bài 2.32 trang 117 SBT giải tích 12Giải bài 2.32 trang 117 sách bài tập giải tích 12. Tìm tập xác định của các hàm số sau:... Đề bài Tìm tập xác định của các hàm số sau: a) \(\displaystyle y = {\log _8}\left( {{x^2} - 3x - 4} \right)\) b) \(\displaystyle y = {\log _{\sqrt 3 }}\left( { - {x^2} + 5x + 6} \right)\) c) \(\displaystyle y = {\log _{0,7}}\dfrac{{{x^2} - 9}}{{x + 5}}\) d) \(\displaystyle y = {\log _{\frac{1}{3}}}\dfrac{{x - 4}}{{x + 4}}\) e) \(\displaystyle y = {\log _\pi }\left( {{2^x} - 2} \right)\) g) \(\displaystyle y = {\log _3}\left( {{3^{x - 1}} - 9} \right)\) Phương pháp giải - Xem chi tiết Hàm số \(\displaystyle y = {\log _a}f\left( x \right)\) xác định khi \(\displaystyle f\left( x \right)\) xác định và \(\displaystyle f\left( x \right) > 0\). Lời giải chi tiết a) ĐKXĐ: \(\displaystyle {x^2} - 3x - 4 > 0\) \(\displaystyle \Leftrightarrow \left( {x + 1} \right)\left( {x - 4} \right) > 0\) \(\displaystyle \Leftrightarrow \left[ \begin{array}{l}x > 4\\x < - 1\end{array} \right.\). Vậy TXĐ \(\displaystyle D = \left( { - \infty ; - 1} \right) \cup \left( {4; + \infty } \right)\). b) ĐKXĐ: \(\displaystyle - {x^2} + 5x + 6 > 0\) \(\displaystyle \Leftrightarrow \left( {x + 1} \right)\left( {6 - x} \right) > 0\) \(\displaystyle \Leftrightarrow - 1 < x < 6\). Vậy TXĐ \(\displaystyle D = \left( { - 1;6} \right)\). c) ĐKXĐ: \(\displaystyle \dfrac{{{x^2} - 9}}{{x + 5}} > 0\) \(\displaystyle \Leftrightarrow \dfrac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{x + 5}} > 0\). Xét dấu vế trái ta được:
Vậy TXĐ \(\displaystyle D = \left( { - 5; - 3} \right) \cup \left( {3; + \infty } \right)\). d) ĐKXĐ: \(\displaystyle \dfrac{{x - 4}}{{x + 4}} > 0 \Leftrightarrow \left[ \begin{array}{l}x > 4\\x < - 4\end{array} \right.\). Vậy TXĐ: \(\displaystyle D = \left( { - \infty ; - 4} \right) \cup \left( {4; + \infty } \right)\). e) ĐKXĐ: \(\displaystyle {2^x} - 2 > 0 \Leftrightarrow {2^x} > 2\) \(\displaystyle \Leftrightarrow {2^x} > {2^1} \Leftrightarrow x > 1\). Vậy TXĐ: \(\displaystyle D = \left( {1; + \infty } \right)\). g) ĐKXĐ: \(\displaystyle {3^{x - 1}} - 9 > 0 \Leftrightarrow {3^{x - 1}} > 9\) \(\displaystyle \Leftrightarrow {3^{x - 1}} > {3^2} \Leftrightarrow x - 1 > 2\) \(\displaystyle \Leftrightarrow x > 3\). Vậy TXĐ: \(\displaystyle D = \left( {3; + \infty } \right)\). HocTot.XYZ
|