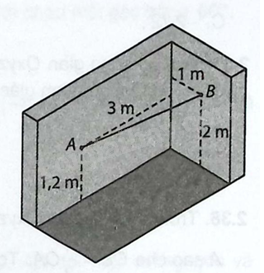
Giải bài 2.32 trang 55 sách bài tập toán 12 - Kết nối tri thứcHình bên mô tả hai bức tường gạch được xây vuông góc với nhau và cùng vuông góc với mặt đất. Một người thợ xây căng dây giữa hai bức tường. Đầu A của sợi dây nằm trên bức tường thứ nhất, cách bức tường thứ 2 là 3 m và cách mặt đất là 1,2 m. Đầu B của sợi dây nằm trên bức tường thứ 2, cách bức tường thứ nhất là 1 m và cách mặt đất là 2 m. a) Hãy lập một hệ trục tọa độ phù hợp và tìm tọa độ của hai đầu (A,B) trong hệ tọa độ đó. b) Tính độ dài của sợi dây được căng. Đề bài Hình bên mô tả hai bức tường gạch được xây vuông góc với nhau và cùng vuông góc với mặt đất. Một người thợ xây căng dây giữa hai bức tường. Đầu A của sợi dây nằm trên bức tường thứ nhất, cách bức tường thứ 2 là 3 m và cách mặt đất là 1,2 m. Đầu B của sợi dây nằm trên bức tường thứ 2, cách bức tường thứ nhất là 1 m và cách mặt đất là 2 m. a) Hãy lập một hệ trục tọa độ phù hợp và tìm tọa độ của hai đầu A, B trong hệ tọa độ đó. b) Tính độ dài của sợi dây được căng.
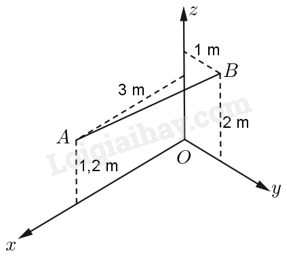
Phương pháp giải - Xem chi tiết Ý a: Theo mối quan hệ vuông góc giữa ba mặt (đôi một vuông góc) gồm hai bức tường và mặt đất ta lập được hệ trục tọa độ. Sau khi lập, quan sát hình vẽ ta xác định được tọa độ các điểm A, B. Ý b: Độ dài sợi dây là độ dài đoạn AB, áp dụng công thức khoảng cách giữa hai điểm để tính. Lời giải chi tiết a) Chọn hệ trục tọa độ như hình vẽ, trong đó \(O\) là góc tường, giao của hai mặt bên là tia \(Oz\), giao của mặt bên và đáy lần lượt là hai tia \(Ox,{\rm{ }}Oy\). Khi đó \(A\left( {3;0;1,2} \right)\) và \(B\left( {0;1;2} \right)\).
b) Độ dài của sợi dây được căng là \(AB = \sqrt {9 + 1 + {{0,8}^2}} = \frac{{\sqrt {266} }}{5} \approx 3,26\) m.
|