Bài 2.39 trang 65 SBT hình học 12Giải bài 2.39 trang 65 sách bài tập hình học 12. Cho tứ diện đều ABCD. Khi quay tứ diện đó xung quanh trục là AB có bao nhiêu hình nón khác nhau được tạo thành?... Đề bài Cho tứ diện đều \(ABCD\). Khi quay tứ diện đó xung quanh trục là \(AB\) có bao nhiêu hình nón khác nhau được tạo thành? A. Một B. Hai C. Ba D. Không có hình nón nào. Phương pháp giải - Xem chi tiết Khi quay tam giác vuông quanh một cạnh góc vuông ta được một hình nón. Lời giải chi tiết
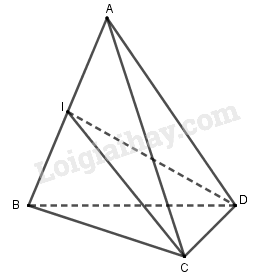
Gọi \(I\) là trung điểm của \(AB\). Dễ thấy \(DI,CI\) vuông góc \(AB\) và \(DI = CI\). Tam giác \(AID\) vuông tại \(I\) nên khi quay quanh \(AI\) ta được hình nón đỉnh \(A\), bán kính đáy \(IC\) và chiều cao \(AI\). Tam giác \(BIC\) vuông tại \(I\) nên khi quay quanh \(BI\) ta được hình nón đỉnh \(B\), bán kính đáy \(IC\) và chiều cao \(BI\). Rõ ràng \(IC = ID\) nên khi quay quanh \(AB\) thì các tam giác \(AID\) và \(BID\) cũng tạo thành hai hình nón như trên. Vậy có hai hình nón. Chọn B. HocTot.XYZ
|