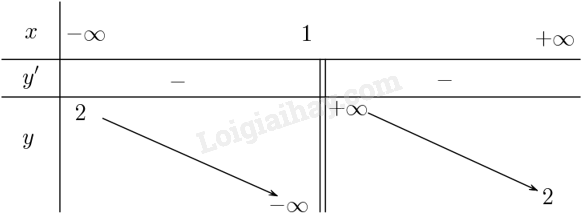
Giải bài 24 trang 51 sách bài tập toán 12 - Kết nối tri thứca) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số (y = frac{{2x - 1}}{{x - 1}}). Tìm tọa độ tâm đối xứng I của đồ thị. b) Tìm điều kiện của tham số m để đường thẳng (d:y = - x + m) cắt đồ thị (H) tại hai điểm phân biệt. c) Chứng minh rằng tiếp tuyến của đồ thị (H) tại mọi điểm M thuộc (H) luôn cắt hai tiệm cận của (H) tại hai điểm A và B và diện tích tam giác IAB không đổi. Đề bài a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số \(y = \frac{{2x - 1}}{{x - 1}}\). Tìm tọa độ tâm đối xứng I của đồ thị. b) Tìm điều kiện của tham số m để đường thẳng \(d:y = - x + m\) cắt đồ thị (H) tại hai điểm phân biệt. c) Chứng minh rằng tiếp tuyến của đồ thị (H) tại mọi điểm M thuộc (H) luôn cắt hai tiệm cận của (H) tại hai điểm A và B và diện tích tam giác IAB không đổi. Phương pháp giải - Xem chi tiết Ý a: Tìm tập xác định, xét dấu đạo hàm, tính các giới hạn tại vô cực, tìm tiệm cận (nếu có), lập bảng biến thiên và vẽ đồ thị. Tâm đối xứng là giao điểm của tiệm cận đứng và tiệm cận ngang. Ý b: Xét phương trình hoành độ giao điểm của đồ thị và đường thẳng. Tìm m để phương trình đó có hai nghiệm phân biệt. Ý c: Điểm M bất kỳ thuộc đồ thị nên có tọa độ phụ thuộc một tham số. Viết phương trình tiếp tuyến tại M và tìm giao điểm A, B. Từ đó chứng minh diện tích tam giác không đổi. Lời giải chi tiết a) Tập xác định: \(\mathbb{R}\backslash \left\{ 1 \right\}\). Sự biến thiên: Ta có \(y' = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0,{\rm{ }}\forall x \ne 1\) suy ra hàm số đồng biến trên từng khoảng của tập xác định. Hàm số không có cực trị. Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } y = 2\), \(\mathop {\lim }\limits_{x \to - \infty } y = 2\) suy ra đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số; \(\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty \), \(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty \) suy ra đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số. Ta có bảng biến thiên:
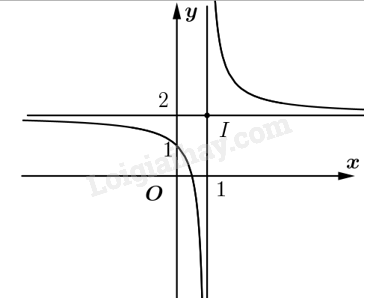
Đồ thị hàm số:
Đồ thị nhận điểm \(I\left( {1;2} \right)\) làm tâm đối xứng. b) Xét phương trình hoành độ giao điểm của d và (H): \( - x + m = \frac{{2x - 1}}{{x - 1}} \Leftrightarrow {x^2} + \left( {1 - m} \right)x + m - 1 = 0{\rm{ }}\left( {x \ne 1} \right)\). Đường thẳng d cắt đồ thị hàm số (H) tại hai điểm phân biệt khi phương trình trên có hai nghiệm phân biệt khác 1. Tương đương với \(\left\{ \begin{array}{l}\Delta > 0\\1 + 1 - m + m - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {1 - m} \right)^2} - 4\left( {m - 1} \right) > 0\\1 \ne 0\end{array} \right. \Leftrightarrow {m^2} - 6m + 5 > 0\) \( \Leftrightarrow m \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\). c) Giả sử \(M\left( {t;\frac{{2t - 1}}{{t - 1}}} \right)\) thuộc (H) với \(t \ne 1\). Phương trình tiếp tuyến của đồ thị (H) tại điểm M là \(\Delta :y = y'\left( t \right)\left( {x - t} \right) + y\left( t \right) \Leftrightarrow y = \frac{{ - 1}}{{{{\left( {t - 1} \right)}^2}}}\left( {x - t} \right) + \frac{{2t - 1}}{{t - 1}}\).
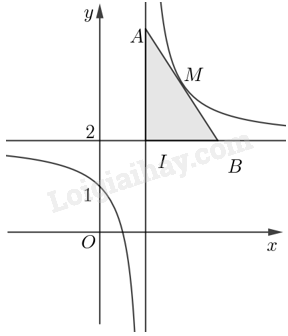
Tiếp tuyến cắt tiệm cận đứng tại \(A\left( {1;\frac{{2t}}{{t - 1}}} \right)\), cắt tiệm cận ngang tại \(B\left( {2t - 1;2} \right)\). Ta có \(IA = \frac{2}{{\left| {t - 1} \right|}}\), \(IB = 2\left| {t - 1} \right|\). Suy ra diện tích tam giác IAB là \(\frac{1}{2}IA \cdot IB = \frac{1}{2} \cdot \frac{2}{{\left| {t - 1} \right|}} \cdot 2\left| {t - 1} \right| = 2\).
|