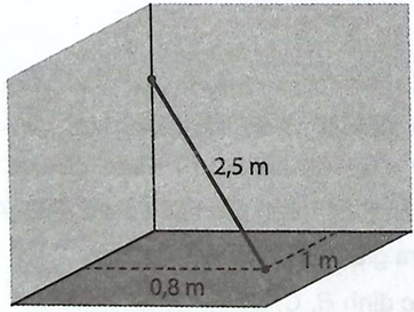
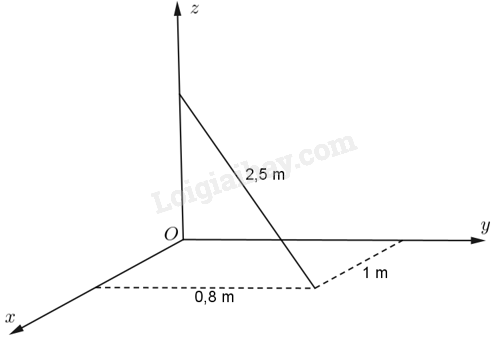
Giải bài 2.48 trang 58 sách bài tập toán 12 - Kết nối tri thứcMột chiếc gậy có chiều dài 2,5 m được đặt trong góc phòng như hình sau đây. Một đầu của chiếc gậy nằm trên sàn nhà, cách hai bức tường lần lượt là 1 m và 0,8 m. Đầu còn lại của chiếc gậy nằm trên mép tường. Đề bài Một chiếc gậy có chiều dài 2,5 m được đặt trong góc phòng như hình sau đây. Một đầu của chiếc gậy nằm trên sàn nhà, cách hai bức tường lần lượt là 1 m và 0,8 m. Đầu còn lại của chiếc gậy nằm trên mép tường. a) Hãy lập một hệ tọa độ \(Oxyz\) phù hợp và tìm tọa độ của đầu gậy nằm trên sàn nhà. b) Tính khoảng cách từ đầu gậy trên mép tường đến sàn nhà. Phương pháp giải - Xem chi tiết Ý a: Lập hệ trục tọa độ dựa trên các yếu tố vuông góc. Ý b: Gọi tọa độ điểm trên mép tường theo một tham số, tìm tham số đó và tìm khoảng cách. Lời giải chi tiết a) Ta lập hệ trục tọa độ như hình vẽ sau: Suy ra đầu gậy trên sàn nhà có tọa độ là \(\left( {1;0,8;0} \right)\). b) Ta thấy đầu gậy trên mép tường là một điểm thuộc tia \(Oz\) nên ta có thể sử điểm đó có tọa là \(\left( {0;0;a} \right)\) với \(a > 0\) đồng thời cũng có \(a\) chính là khoảng cách từ đầu gậy trên mép tường đến sàn nhà. Mặt khác chiếc gậy có chiều dài 2,5 m, do đó ta có \(\sqrt {1 + {{0,8}^2} + {a^2}} = 2,5 \Leftrightarrow \sqrt {{a^2} + 1,64} = 2,5 \Leftrightarrow a = \frac{{\sqrt {461} }}{{10}} \approx 2,15\). Vậy khoảng cách từ đầu gậy trên mép tường đến sàn nhà \(2,15\) m.
|