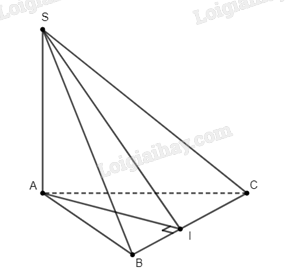
Giải bài 26 trang 99 sách bài tập toán 11 - Cánh diềuCho hình chóp (S.ABC) có (SA bot left( {ABC} right)). Gọi (I) là hình chiếu của (A) trên đường thẳng (BC) Đề bài Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(I\) là hình chiếu của \(A\) trên đường thẳng \(BC\), \(\alpha \) là góc giữa đường thẳng \(SI\) và mặt phẳng \(\left( {ABC} \right)\), \(\beta \) là số đo của góc nhị diện \(\left[ {S,BC,A} \right]\). Phát biểu nào sau đây là đúng? A. \(\alpha = {90^o} - \beta \) B. \(\alpha = {180^o} - \beta \) C. \(\alpha = {90^o} + \beta \) D. \(\alpha = \beta \) Phương pháp giải - Xem chi tiết Vẽ hình, chỉ ra góc \(\alpha \) và \(\beta \) trên hình vẽ rồi so sánh chúng. Lời giải chi tiết
Do \(SA \bot \left( {ABC} \right)\), ta suy ra hình chiếu của \(S\) trên \(\left( {ABC} \right)\) là điểm \(A\). Suy ra góc giữa \(SI\) và \(\left( {ABC} \right)\) chính là góc \(\widehat {SIA}\), tức là \(\alpha = \widehat {SIA}\). Mặt khác, do \(SA \bot \left( {ABC} \right)\), ta suy ra \(SA \bot BC\). Mà theo đề bài, \(AI \bot BC\) nên ta suy ra \(\left( {SAI} \right) \bot BC\), từ đó \(SI \bot BC\). Như vậy, do \(SI \bot BC\), \(AI \bot BC\), nên \(\widehat {SIA}\) chính là góc phẳng nhị diện của góc nhị diện \(\left[ {S,BC,A} \right]\), tức là \(\beta = \widehat {SIA}\). Vậy ta suy ra \(\alpha = \beta \). Đáp án đúng là D.
|