Bài 2.61 trang 132 SBT giải tích 12Giải bài 2.61 trang 132 sách bài tập giải tích 12. Giải các bất phương trình sau bằng đồ thị:...
Lựa chọn câu để xem lời giải nhanh hơn
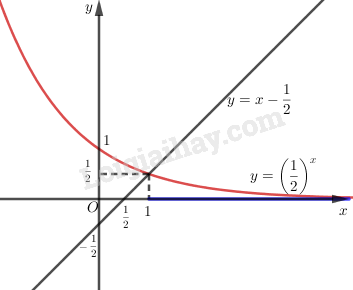
Giải các bất phương trình sau bằng đồ thị: LG a \(\displaystyle {\left( {\frac{1}{2}} \right)^x} < x - \frac{1}{2}\) Phương pháp giải: - Vẽ đồ thị hàm số \(\displaystyle y = {\left( {\frac{1}{2}} \right)^x}\left( C \right)\) và đường thẳng \(\displaystyle y = x - \frac{1}{2}\left( d \right)\) trên cùng một mặt phẳng tọa độ. - Quan sát đồ thị, nghiệm của bất phương trình là phần \(\displaystyle x\) mà ứng với nó thì đồ thị \(\displaystyle \left( C \right)\) nằm phía dưới đường thẳng \(\displaystyle d\). Giải chi tiết: Vẽ đồ thị của hàm số \(\displaystyle y = {\left( {\frac{1}{2}} \right)^x}\) và đường thẳng \(\displaystyle y = x - \frac{1}{2}\) trên cùng một hệ trục tọa độ. Ta thấy chúng cắt nhau tại điểm có hoành độ \(\displaystyle x = 1\). Với \(\displaystyle x > 1\) đồ thị của hàm số \(\displaystyle y = {\left( {\frac{1}{2}} \right)^x}\) nằm phía dưới đường thẳng \(\displaystyle y = x - \frac{1}{2}\). Vậy tập nghiệm của bất phương trình đã cho là \(\displaystyle (1; + \infty )\)
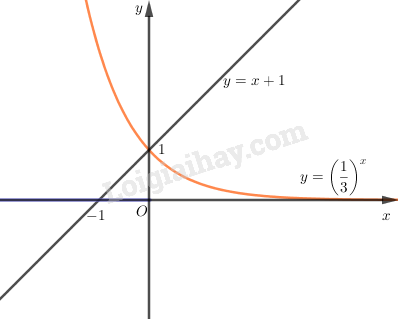
LG b \(\displaystyle {\left( {\frac{1}{3}} \right)^x} \ge x + 1\) Phương pháp giải: - Vẽ đồ thị hàm số \(\displaystyle y = {\left( {\frac{1}{3}} \right)^x}\left( C \right)\) và đường thẳng \(\displaystyle y = x + 1\left( d \right)\) trên cùng một mặt phẳng tọa độ. - Quan sát đồ thị, nghiệm của bất phương trình là phần \(\displaystyle x\) mà ứng với nó thì đồ thị \(\displaystyle \left( C \right)\) nằm phía trên đường thẳng \(\displaystyle d\). Giải chi tiết: Vẽ đồ thị của hàm số \(\displaystyle y = {\left( {\frac{1}{3}} \right)^x}\) và đường thẳng \(\displaystyle y = x + 1\) trên cùng một hệ trục tọa độ. Ta thấy chúng cắt nhau tại điểm có hoành độ \(\displaystyle x = 0\). Khi \(\displaystyle x < 0\) đồ thị của hàm số \(\displaystyle y = {\left( {\frac{1}{3}} \right)^x}\) nằm phía trên đường thẳng \(\displaystyle y = x + 1\). Vậy tập nghiệm của bất phương trình đã cho là \(\displaystyle ( - \infty ;0]\).
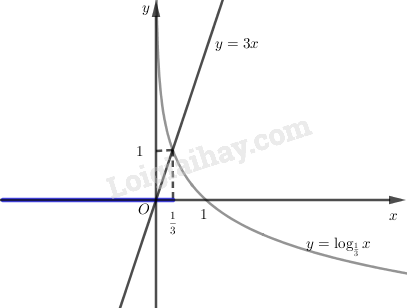
LG c \(\displaystyle {\log _{\frac{1}{3}}}x > 3x\) Phương pháp giải: - Vẽ đồ thị hàm số \(\displaystyle y = {\log _{\frac{1}{3}}}x\left( C \right)\) và đường thẳng \(\displaystyle y = 3x\left( d \right)\) trên cùng một mặt phẳng tọa độ. - Quan sát đồ thị, nghiệm của bất phương trình là phần \(\displaystyle x\) mà ứng với nó thì đồ thị \(\displaystyle \left( C \right)\) nằm phía trên đường thẳng \(\displaystyle d\). Giải chi tiết: Vẽ đồ thị của hàm số \(\displaystyle y = {\log _{\frac{1}{3}}}x\) và đường thẳng \(\displaystyle y = 3x\) trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ \(\displaystyle x = \frac{1}{3}\). Khi \(\displaystyle x < \frac{1}{3}\) đồ thị của hàm số \(\displaystyle y = {\log _{\frac{1}{3}}}x\) nằm phía trên đường thẳng \(\displaystyle y = 3x\). Vậy tập nghiệm của bất phương trình đã cho là \(\displaystyle \left( { - \infty ;\frac{1}{3}} \right)\).
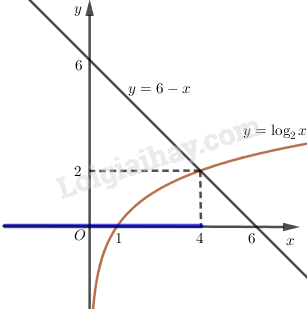
LG d \(\displaystyle {\log _2}x \le 6 - x\) Phương pháp giải: - Vẽ đồ thị hàm số \(\displaystyle y = {\log _2}x\left( C \right)\) và đường thẳng \(\displaystyle y = 6 - x\left( d \right)\) trên cùng một mặt phẳng tọa độ. - Quan sát đồ thị, nghiệm của bất phương trình là phần \(\displaystyle x\) mà ứng với nó thì đồ thị \(\displaystyle \left( C \right)\) nằm phía dưới đường thẳng \(\displaystyle d\). Giải chi tiết: Vẽ đồ thị của hàm số \(\displaystyle y = {\log _2}x\) và đường thẳng \(\displaystyle y = 6 - x\) trên cùng một hệ trục tọa độ. Ta thấy chúng cắt nhau tại điểm có hoành độ \(\displaystyle x = 4\). Khi \(\displaystyle x < 4\), đồ thị của hàm số \(\displaystyle y = {\log _2}x\) nằm phía dưới \(\displaystyle y = 6 - x\) . Vậy tập nghiệm của bất phương trình đã cho là \(\displaystyle ( - \infty ;4]\).
HocTot.XYZ
|