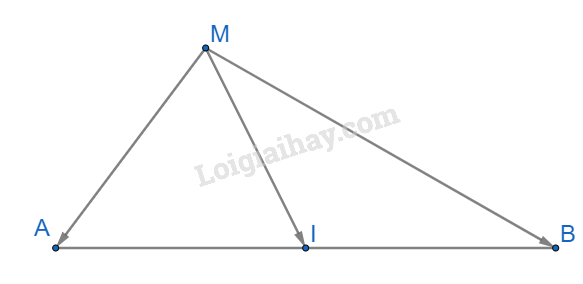
Giải bài 3 trang 97 sách bài tập toán 10 - Chân trời sáng tạoLấy một điểm M tùy ý. Chứng minh rằng: Đề bài Lấy một điểm M tùy ý. Chứng minh rằng: a) I là trung điểm của đoạn thẳng AB khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) b) G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) Lời giải chi tiết a)
Áp dụng quy tắc ba điểm ta có: \(\overrightarrow {MA} + \overrightarrow {MB} = \left( {\overrightarrow {MI} + \overrightarrow {IA} } \right) + \left( {\overrightarrow {MI} + \overrightarrow {IB} } \right) = 2\overrightarrow {MI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) = 2\overrightarrow {MI} \) (đpcm) (I là trung điểm của AB nên \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \) b)
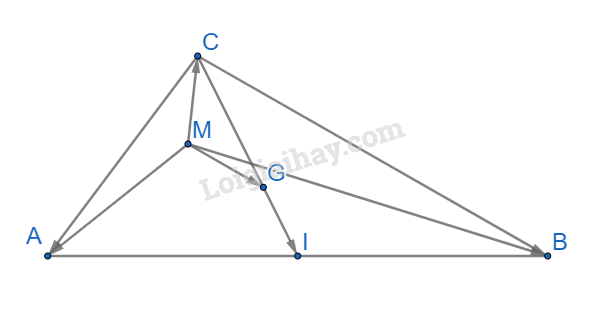
Áp dụng quy tắc ba điểm ta có: \(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \left( {\overrightarrow {MG} + \overrightarrow {GA} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GB} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GC} } \right)\\ = 3\overrightarrow {MG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = 3\overrightarrow {MG} \end{array}\) (đpcm) (G là trọng tâm của ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \))
|