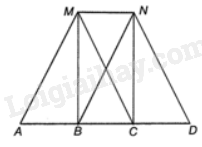
Giải bài 3.12 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sốngXét hai hình bình hành MNBA và MNCB. a) Chứng minh A, B, C là ba điểm thẳng hàng; Đề bài Xét hai hình bình hành MNBA và MNCB. a) Chứng minh A, B, C là ba điểm thẳng hàng; b) Chứng minh B là trung điểm của AC; c) Hỏi tam giác MAB thỏa mãn điều kiện gì để MNCA là một hình thang cân? d) Lấy điểm D để tứ giác MNDC là hình bình hành. Hỏi tam giác MAB thỏa mãn điều kiện gì để MNDA là một hình thang cân? Phương pháp giải - Xem chi tiết a) Sử dụng kiến thức tính chất hình bình hành để chứng minh: Hình bình hành có các cạnh đối song song. b) Sử dụng kiến thức tính chất hình bình hành để chứng minh: Hình bình hành có các cạnh đối bằng nhau. c, d) Sử dụng kiến thức dấu hiệu nhận biết hình thang cân để tìm điều kiện: Hình thang có hai góc kề một đáy bằng nhau là hình thang cân. Lời giải chi tiết
a) Vì tứ giác MNBA là hình bình hành nên MN//AB Vì tứ giác MNCB là hình bình hành nên MN//BC Do đó, AB và BC trùng nhau (tiên đề Euclid) Vậy A, B, C thẳng hàng. b) Vì tứ giác MNBA là hình bình hành nên \(MN = AB\) Vì tứ giác MNCB là hình bình hành nên \(MN = BC\) Do đó, \(AB = BC\) Mà A, B, C thẳng hàng nên B là trung điểm của AC. c) Vì MNCB là hình bình hành nên NC//MB Do đó, \(\widehat {NCB} = \widehat {MBA}\) (hai góc đồng vị) (1) Để MNCA là hình thang cân thì \(\widehat {NCB} = \widehat {MAB}\) (2) Từ (1) và (2) ta có: \(\widehat {MAB} = \widehat {MBA}\) Do đó, tam giác MAB cân tại M. Vậy để MNCA là hình thang cân thì cần thêm điều kiện tam giác MAB cân tại M. d) Vì MNDC là hình bình hành nên MC//ND. Do đó, \(\widehat D = \widehat {MCA}\) Điều kiện để MNDA là hình thang cân là \(\widehat A = \widehat D\) Suy ra, \(\widehat {MCA} = \widehat A\). Khi đó, tam giác MCA cân tại M. Mà MB là trung tuyến của tam giác nên MB là đường cao của tam giác, hay \(MB \bot AB\) tại B. Vậy để MNDA là một hình thang cân thì tam giác AMB vuông tại B.
|