Giải bài 3.3 trang 37 SGK Toán 10 tập 1 – Kết nối tri thứcChứng minh các hệ thức sau:
Lựa chọn câu để xem lời giải nhanh hơn
Chứng minh các hệ thức sau: a) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\). b) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\) c) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha < {180^o})\) LG a a) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\). Phương pháp giải: Bước 1: Vẽ đường tròn lượng giác, lấy điểm M biểu diễn góc \(\alpha \) bất kì. Bước 2: Xác định \(\sin \alpha ,\;\cos \alpha \)( tương ứng với tung độ và hoành độ của điểm M). Bước 3: Suy ra đẳng thức cần chứng minh. Lời giải chi tiết:
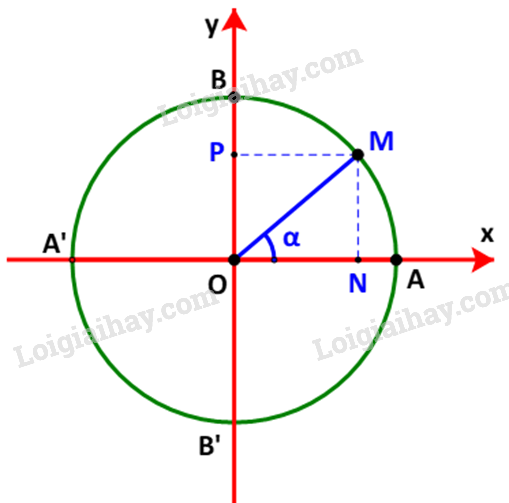
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy. Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha = {x^2}\\{\sin ^2}\alpha = {y^2}\end{array} \right.\)(1) Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2) Từ (1) và (2) suy ra \({\sin ^2}\alpha + {\cos ^2}\alpha = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N) \( \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (vì OM = 1). (đpcm) LG b b) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\) Phương pháp giải: Bước 1: Viết \(\tan \alpha \) dưới dạng \(\frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\), thay vào vế trái. Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải. Lời giải chi tiết: Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\) \( \Rightarrow 1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\) Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \) \( \Rightarrow 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm) LG c c) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha < {180^o})\) Phương pháp giải: Bước 1: Viết \(\cot \alpha \) dưới dạng \(\frac{{\cos \alpha }}{{\sin \alpha }}\;\), thay vào vế trái. Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải. Lời giải chi tiết: Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha < {180^o})\) \( \Rightarrow 1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\) Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \) \( \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)
|