Bài 3.45 trang 132 SBT hình học 12Giải bài 3.45 trang 132 sách bài tập hình học 12. Cho hai đường thẳng... Đề bài Cho hai đường thẳng d1: \(\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{{ - 3}} = \dfrac{{z - 5}}{4}\) và d2: \(\left\{ {\begin{array}{*{20}{c}}{x = 7 + 3t}\\{y = 2 + 2t}\\{z = 1 - 2t}\end{array}} \right.\) a) Chứng minh rằng d1 và d2 cùng nằm trong một mặt phẳng \((\alpha )\). b) Viết phương trình của \((\alpha )\). Phương pháp giải - Xem chi tiết Sử dụng vị trí tương đối giữa hai đường thẳng. Xem chi tiết tại đây. Lời giải chi tiết
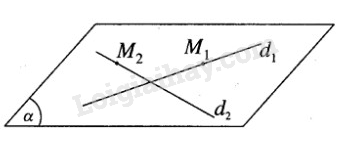
a) Ta có \(\overrightarrow {{u_{{d_1}}}} = \left( {2; - 3;4} \right)\) và \(\overrightarrow {{u_{{d_2}}}} = (3;2; - 2)\) \(\overrightarrow n = \left[ {\overrightarrow {{u_{{d_1}}}} ,\overrightarrow {{u_{{d_2}}}} } \right] = ( - 2;16;13)\) Lấy điểm M1(1; -2; 5) trên d1 và điểm M2(7;2;1) trên d2. Ta có \(\overrightarrow {{M_1}{M_2}} = (6;4; - 4)\); \(\overrightarrow n .\overrightarrow {{M_1}{M_2}} = - 12 + 64 - 52 = 0\) Suy ra \({d_1}\) và \({d_2}\) cùng nằm trong mặt phẳng \((\alpha )\) b) Mặt phẳng \((\alpha )\) chứa \({M_1}\) và có vecto pháp tuyến là \(\overrightarrow n \) , vậy phương trình của \((\alpha )\) là: \(– 2(x – 1) +16(y + 2) + 13(z – 5) = 0\) hay \(2x – 16y – 13z + 31 = 0\). HocTot.XYZ
|