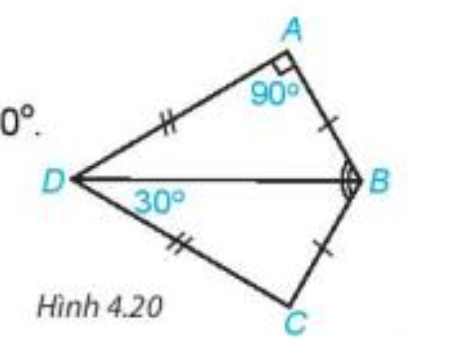
Giải bài 3(4.6) trang 59 vở thực hành Toán 7Bài 3 (4.6). Cho các điểm A, B, C, D như hình vẽ bên. a) Chứng minh \(\Delta ABD = \Delta CBD\) b) Biết rằng \(\widehat {BAD} = {90^o},\widehat {CDB} = {30^o}\), hãy tính \(\widehat {ABC}\). Đề bài Bài 3 (4.6). Cho các điểm A, B, C, D như hình vẽ bên. a) Chứng minh \(\Delta ABD = \Delta CBD\) b) Biết rằng \(\widehat {BAD} = {90^o},\widehat {CDB} = {30^o}\), hãy tính \(\widehat {ABC}\).
Phương pháp giải - Xem chi tiết Chỉ ra các cặp cạnh tương ứng bằng nhau của hai tam giác Lời giải chi tiết a) Hai tam giác ABD và CBD có: AD = DC và AB = BC (theo giả thiết), BD là cạnh chung Do đó \(\Delta ABD = \Delta CBD\left( {c.c.c} \right)\) b) Vì \(\Delta ABD = \Delta CBD\) nên \(\widehat {ADB} = \widehat {CDB} = {30^o}\) Do tổng ba góc trong tam giác ABD bằng \({180^o}\) nên ta có \(\widehat {ABD} + \widehat {BAD} + \widehat {ADB} = {180^o} \Rightarrow \widehat {ABD} = {180^o} - \widehat {BAD} - \widehat {ADB} = {180^o} - {90^o} - {30^o} = {60^o}\) Lại vì \(\Delta ABD = \Delta CBD\) nên \(\widehat {CBD} = \widehat {ABD} = {60^o}\) Từ đây ta được \(\widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {120^o}\)
|