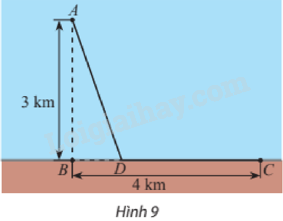
Giải bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạoMột giếng dầu ngoài khơi được đặt ở vị trí \(A\) cách bờ biển 3 km, \(B\) là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí \(C\) trên bờ biển, cách vị trí \(B\) một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng \(AD\) và \(DC\) (\(D\) là một vị trí nằm giữa \(B\) và \(C\)). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của \(D\) như thế nào để giảm thiểu chi p Đề bài Một giếng dầu ngoài khơi được đặt ở vị trí \(A\) cách bờ biển 3 km, \(B\) là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí \(C\) trên bờ biển, cách vị trí \(B\) một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng \(AD\) và \(DC\) (\(D\) là một vị trí nằm giữa \(B\) và \(C\)). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của \(D\) như thế nào để giảm thiểu chi phí lắp đặt nhất?
Phương pháp giải - Xem chi tiết • Đặt \(BD = x\), biểu thị chi phí lắp đặt thông qua các đại lượng đã biết và ẩn. • Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\): Bước 1. Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó \(f'\left( x \right)\) bằng 0 hoặc không tồn tại. Bước 2. Tính \(f\left( a \right);f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right);f\left( b \right)\). Bước 3. Gọi \(M\) là số lớn nhất và \(m\) là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\). Lời giải chi tiết Đặt \(BD = x\left( {km} \right)\left( {0 \le x \le 4} \right)\). Gọi \(a\) là chi phí lắp đặt cho mỗi kilômét đường ống đặt trên bờ. Khi đó \(2a\) là chi phí lắp đặt cho mỗi kilômét đường ống đặt dưới biển. Ta có: \(C{\rm{D}} = BC - B{\rm{D}} = 4 - x,A{\rm{D}} = \sqrt {A{B^2} + B{{\rm{D}}^2}} = \sqrt {{x^2} + 9} \). Chi phí lắp đặt đường ống là: \(2{\rm{a}}\sqrt {{x^2} + 9} + a\left( {4 - x} \right) = a\left( {2\sqrt {{x^2} + 9} + 4 - x} \right)\). Xét hàm số \(f\left( x \right) = 2\sqrt {{x^2} + 9} + 4 - x\) trên đoạn \(\left[ {0;4} \right]\). Ta có: \(f'\left( x \right) = 2.\frac{{{{\left( {{x^2} + 9} \right)}^\prime }}}{{2\sqrt {{x^2} + 9} }} - 1 = \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} - 1\) \(f'\left( x \right) = 0 \Leftrightarrow \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} - 1 = 0 \Leftrightarrow \frac{{2{\rm{x}}}}{{\sqrt {{x^2} + 9} }} = 1 \Leftrightarrow \sqrt {{x^2} + 9} = 2{\rm{x}} \Leftrightarrow {x^2} + 9 = 4{{\rm{x}}^2} \Leftrightarrow {{\rm{x}}^2} = 3 \Leftrightarrow x = \sqrt 3 \) hoặc \(x = - \sqrt 3 \) (loại). \(f\left( 0 \right) = 10;f\left( {\sqrt 3 } \right) = 4 + 3\sqrt 3 ;f\left( 4 \right) = 10\). Vậy \(\mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( {\sqrt 3 } \right) = 4 + 3\sqrt 3 \). Vậy chi phí lắp đặt thấp nhất khi \(x = \sqrt 3 \approx 1,7\left( {km} \right)\).
|