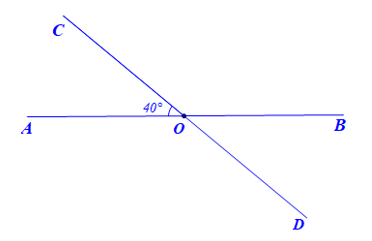
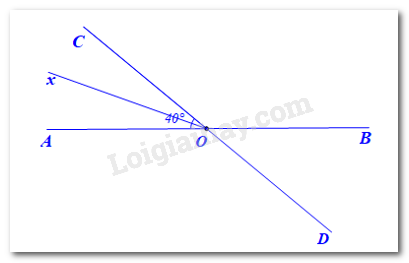
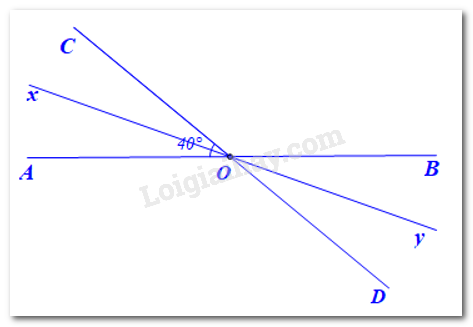
Giải Bài 4 trang 79 sách bài tập toán 7 tập 1 - Chân trời sáng tạoCho hai đường thẳng AB và CD cắt nhau tại O tạo thành Đề bài Cho hai đường thẳng AB và CD cắt nhau tại O tạo thành \(\widehat {AOC}\)=40°. a) Tính số đo các góc còn lại. b) Vẽ Ox là tia phân giác của \(\widehat {AOC}\). Hãy tính số đo của \(\widehat {xOD}\) và \(\widehat {xOB}\) c) Vẽ Oy là tia đối của tia Ox. Chứng tỏ rằng Oy là tia phân giác của \(\widehat {BOD}\) Phương pháp giải - Xem chi tiết Ta sử dụng tính chất 2 góc kề bù và 2 góc đối đỉnh để tính số đo các góc còn lại Lời giải chi tiết
a) Ta có: • \(\widehat {AOC}\) và \(\widehat {BOD}\) là hai góc đối đỉnh nên: \(\widehat {AOC}\)=\(\widehat {BOD}\)=40°. • \(\widehat {AOC}\) và \(\widehat {BOC}\) là hai góc kề bù nên: \(\widehat {AOC}\)+\(\widehat {BOC}\)=180°. Suy ra \(\widehat {BOC}\)=180°−\(\widehat {AOD}\)=180°−40°=140° • \(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh nên: \(\widehat {AOD}\)=\(\widehat {BOC}\)=140° Vậy \(\widehat {BOD}\)=40°, \(\widehat {BOC}\)=140° và \(\widehat {AOD}\)=140° b)
• Vì tia Ox là tia phân giác của \(\widehat {AOC}\) nên ta có: \(\widehat {AOx}\)=\(\widehat {xOC}\)=\(\dfrac{1}{2}\)\(\widehat {AOC}\)=\(\dfrac{1}{2}\).40°=20°. • Vì \(\widehat {AOx}\) và \(\widehat {AOD}\) là hai góc kề nhau nên ta có: \(\widehat {AOx}\)+\(\widehat {AOD}\)=\(\widehat {xOD}\) Suy ra \(\widehat {xOD}\) =20°+140°=160°. • Vì \(\widehat {xOC}\) và \(\widehat {BOC}\) là hai góc kề nhau nên ta có: \(\widehat {xOC}\)+\(\widehat {BOC}\)=\(\widehat {xOB}\) Suy ra \(\widehat {xOB}\)=20°+140°=160°. Vậy \(\widehat {xOD}\)=160°,\(\widehat {xOB}\)=160° c)
Ta có • \(\widehat {xOA}\) và \(\widehat {yOD}\) là hai góc đối đỉnh nên: \(\widehat {xOA}\)=\(\widehat {yOD}\). Mà \(\widehat {xOA}=20^0\) nên \(\widehat {yOD}\) =20°. • \(\widehat {xOC}\) và \(\widehat {yOB}\) là hai góc đối đỉnh nên: \(\widehat {xOC}\)=\(\widehat {yOB}\). Mà \(\widehat {xOC}=20^0\) nên \(\widehat {yOB}\) =20°. Suy ra \(\widehat {yOB}\) =\(\widehat {yOD}=\dfrac{1}{2}.\widehat {BOD}(=20^0)\) Vậy tia Oy là tia phân giác của \(\widehat {BOD}\)
|