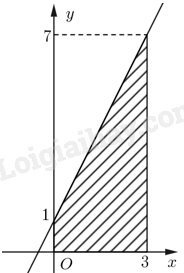
Giải bài 4.11 trang 12 sách bài tập toán 12 - Kết nối tri thứcSử dụng ý nghĩa hình học của tích phân, tính: a) (intlimits_0^3 {left( {2x + 1} right)dx} ); b) (intlimits_0^4 {sqrt {16 - {x^2}} dx} ). Đề bài Sử dụng ý nghĩa hình học của tích phân, tính: a) \(\int\limits_0^3 {\left( {2x + 1} \right)dx} \); b) \(\int\limits_0^4 {\sqrt {16 - {x^2}} dx} \). Phương pháp giải - Xem chi tiết Ý a: Giá trị tích phân là diện tích của hình vẽ giới hạn bởi hàm \(2x + 1\) và hai đường thẳng xác định bởi giá trị hai cận do hàm không âm trên \(\left[ {0;3} \right]\). Xác định hình vẽ đó và tính diện tích bằng công thức hình học. Ý b: Giá trị tích phân là diện tích của hình vẽ giới hạn bởi hàm \(\sqrt {16 - {x^2}} \) và hai đường thẳng xác định bởi giá trị hai cận do hàm không âm trên \(\left[ {0;4} \right]\). Xác định hình vẽ đó và tính diện tích bằng công thức hình học. Lời giải chi tiết a) Ta có hàm số \(f\left( x \right) = 2x + 1\) không âm trên đoạn \(\left[ {0;3} \right]\). Do đó tích phân \(\int\limits_0^3 {\left( {2x + 1} \right)dx} \) là diện tích của hình vẽ giới hạn bởi đồ thị \(y = f\left( x \right)\) và hai đường thẳng \(x = 0\) (trục \(Ox\)) và \(x = 3\) như hình vẽ bên. Ta cần tính diện tích hình thang vuông có đáy lớn là 7, đáy bé là 1 và chiều cao là 3. Suy ra \(\int\limits_0^3 {\left( {2x + 1} \right)dx} = \frac{1}{2} \cdot \left( {1 + 7} \right) \cdot 3 = 12\).
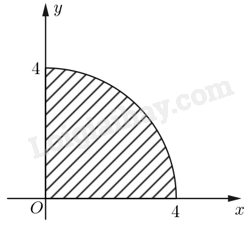
b) Ta có \(\int\limits_0^4 {\sqrt {16 - {x^2}} dx} \). Ta có hàm số \(f\left( x \right) = \sqrt {16 - {x^2}} \) không âm trên đoạn \(\left[ {0;4} \right]\). Do đó tích phân \(\int\limits_0^3 {\left( {2x + 1} \right)dx} \) là diện tích của hình vẽ giới hạn bởi đồ thị \(y = f\left( x \right)\) và hai đường thẳng \(x = 0\) (trục \(Ox\)) và \(x = 4\) như hình vẽ bên. Ta cần tính diện tích một phần tư đường tròn có bán kính là 4, tâm O nằm ở góc phần tư thứ I. Suy ra \(\int\limits_0^4 {\sqrt {16 - {x^2}} dx} = \frac{1}{4} \cdot \pi \cdot {4^2} = 4\pi \).
|