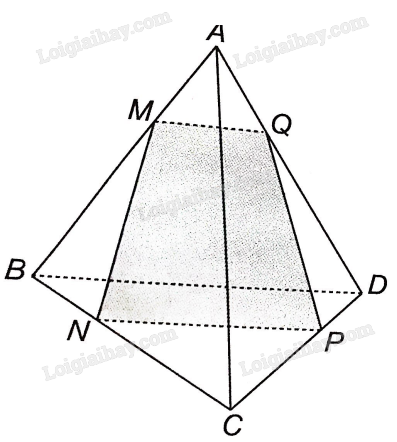
Giải bài 4.13 trang 59 sách bài tập toán 11 - Kết nối tri thức với cuộc sốngCho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD. Đề bài Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD. Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP) trong các trường hợp sau: a, Đường thẳng NP song song với đường thẳng BD. b, Đường thẳng NP cắt BD. Phương pháp giải - Xem chi tiết Dựa vào định lý về 3 đường giao tuyến của 3 mặt phẳng: Nếu có 2 giao tuyến của song song với nhau thì giao tuyến thứ 3 cũng song song với 2 giao tuyến đó. Còn nếu có 2 giao tuyến cắt nhau thì 3 giao tuyến đó đồng quy. Lời giải chi tiết
a,
NP là giao tuyến của hai mặt phẳng (MNP và (BCD BD là giao tuyến của hai mặt phẳng (ABD và (BCD Mà NP // BD nên giao tuyến của (MNP và (ABD cũng là một đường thẳng song song với NP và BD. Ta thấy M thuộc AB nên M là điểm chung của (MNP và (ABD. Vậy giao tuyến của (MNP và (ABD là đường thẳng d đi qua M, song song với NP và BD. Trong mặt phẳng (ABD, gọi Q là giao điểm giữa d và AD. Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP chính là điểm Q. b,
NP là giao tuyến của hai mặt phẳng (MNP) và (BCD) BD là giao tuyến của hai mặt phẳng (ABD) và (BCD) Mà đường thẳng NP và BD cắt nhau nên giao tuyến d của (MNP) và (ABD) là một đường thẳng đồng quy với NP và BD. (gọi R là giao điểm của NP và BD, vậy d đi qua điểm R Ta thấy M thuộc AB nên M là điểm chung của (MNP) và (ABD). Vậy M thuộc đường giao tuyến d. Trong mặt phẳng (BCD) gọi S là giao điểm của MR và BD, vậy giao tuyến d cũng sẽ đi qua điểm S. Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) chính là điểm S.
|