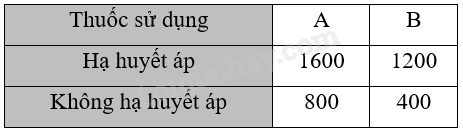
Giải bài 42 trang 55 sách bài tập toán 12 - Kết nối tri thứcNghiên cứu hiệu quả của hai loại thuốc hạ huyết áp A và B trên 4000 người, ta thu được bảng thống kê 2 x 2 sau đây: Chọn ngẫu nhiên một người, tính xác suất để: a) Người đó hạ huyết áp biết rằng người đó dùng thuốc A; b) Người đó dùng thuốc A biết rằng người đó hạ huyết áp; c) Người đó dùng thuốc B biết rằng người đó không hạ huyết áp; d) Người đó không hạ huyết áp biết rằng người đó dùng thuốc B. Đề bài Nghiên cứu hiệu quả của hai loại thuốc hạ huyết áp A và B trên 4000 người, ta thu được bảng thống kê 2 x 2 sau đây:
Chọn ngẫu nhiên một người, tính xác suất để: a) Người đó hạ huyết áp biết rằng người đó dùng thuốc A; b) Người đó dùng thuốc A biết rằng người đó hạ huyết áp; c) Người đó dùng thuốc B biết rằng người đó không hạ huyết áp; d) Người đó không hạ huyết áp biết rằng người đó dùng thuốc B. Phương pháp giải - Xem chi tiết Gọi tên các biến cố, đếm số khả năng xảy ra biến cố. Ý a: Tính xác suất của biến cố. Áp dụng công thức xác suất có điều kiện. Ý b: Tính xác suất của biến cố. Áp dụng công thức xác suất có điều kiện. Ý c: Tính xác suất của biến cố. Áp dụng công thức xác suất có điều kiện. Ý d: Tính xác suất của biến cố. Áp dụng công thức xác suất có điều kiện. Lời giải chi tiết Gọi A là biến cố: “Người đó dùng thuốc A”; B là biến cố: “Người đó dùng thuốc B”; E là biến cố: “Người đó hạ huyết áp”; F là biến cố: “Người đó không hạ huyết áp”; Ta có \(n\left( A \right) = 1600 + 800 = 2400\); \(n\left( B \right) = 1200 + 400 = 1600\); \(n\left( E \right) = 1600 + 1200 = 2800\); \(n\left( F \right) = 800 + 400 = 1200\); \(n\left( {EA} \right) = 1600\); \(n\left( {FB} \right) = 400\). a) Ta có \(P\left( A \right) = \frac{{2400}}{{4000}};{\rm{ P}}\left( {EA} \right) = \frac{{1600}}{{4000}} \Rightarrow P\left( {E|A} \right) = \frac{{{\rm{P}}\left( {EA} \right)}}{{P\left( A \right)}} = \frac{{1600}}{{2400}} = \frac{2}{3}\). b) Ta có \(P\left( E \right) = \frac{{2800}}{{4000}};{\rm{ P}}\left( {EA} \right) = \frac{{1600}}{{4000}} \Rightarrow P\left( {A|E} \right) = \frac{{{\rm{P}}\left( {EA} \right)}}{{P\left( E \right)}} = \frac{{1600}}{{2800}} = \frac{4}{7}\). c) Ta có \(P\left( F \right) = \frac{{1200}}{{4000}};{\rm{ P}}\left( {FB} \right) = \frac{{400}}{{4000}} \Rightarrow P\left( {B|F} \right) = \frac{{{\rm{P}}\left( {FB} \right)}}{{P\left( F \right)}} = \frac{{400}}{{1200}} = \frac{1}{3}\). d) Ta có \(P\left( B \right) = \frac{{1600}}{{4000}};{\rm{ P}}\left( {FB} \right) = \frac{{400}}{{4000}} \Rightarrow P\left( {F|B} \right) = \frac{{{\rm{P}}\left( {FB} \right)}}{{P\left( B \right)}} = \frac{{400}}{{1600}} = \frac{1}{4}\).
|