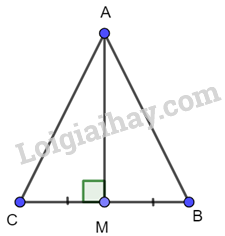
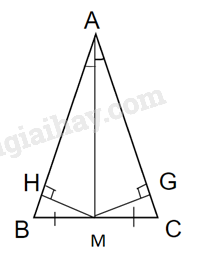
Giải bài 4.25 trang 84 SGK Toán 7 tập 1 - Kết nối tri thứcCho tam giác ABC và M là trung điểm của đoạn thẳng BC. a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A. b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A. Đề bài Cho tam giác ABC và M là trung điểm của đoạn thẳng BC. a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A. b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A. Phương pháp giải - Xem chi tiết a) Chứng minh tam giác hai tam giác AMB và AMC bằng nhau suy ra tam giác ABC cân. b) Từ M kẻ hai đường vuông góc với AC và AB từ đó chứng minh hai góc B và C bằng nhau. Chứng minh hai tam giác AMB và AMC bằng nhau Suy ra tam giác ABC cân Lời giải chi tiết a) Xét 2 tam giác vuông AMC và AMB có: AM chung BM=CM (gt) Suy ra \(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông) Do đó AC=AB (2 cạnh tương ứng) nên tam giác ABC cân tại A b) Kẻ MH vuông góc với AB (H thuộc AB) MG vuông góc với AC (G thuộc AC) Xét 2 tam giác vuông AHM và AGM có: AM chung \(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC) Suy ra \(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn) Do đó HM=GM (2 cạnh tương ứng) Xét 2 tam giác vuông BHM và CGM có: BM=CM (giả thiết) MH=MG (chứng minh trên) Suy ra \(\Delta BHM = \Delta CGM\) (cạnh huyền – cạnh góc vuông) Do đó \(\widehat {HBM} = \widehat {GCM}\) (2 góc tương ứng) Dẫn đến tam giác ABC cân tại A.
|