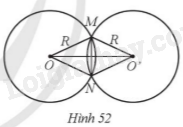
Giải bài 49 trang 123 sách bài tập toán 9 - Cánh diều tập 1Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO' = 24cm và MN = 10 cm (Hình 52). Khi đó, R bằng A. 26 cm. B. 13 cm. C. 14 cm. D. 34 cm Đề bài Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO' = 24cm và MN = 10 cm (Hình 52).
Khi đó, R bằng A. 26 cm. B. 13 cm. C. 14 cm. D. 34 cm. Phương pháp giải - Xem chi tiết Bước 1: Chứng minh \(OMO'N\) là hình thoi, từ đó tính MH, OH. Bước 2: Áp dụng định lý Pythagore trong tam giác OMH để tính R. Lời giải chi tiết
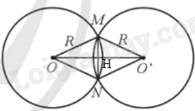
Gọi giao điểm của MN và OO’ là H Do \(OM = ON = O'M = O'N = R\) nên \(OMO'N\) là hình thoi, do đó \(MN \bot OO'\) và \(MH = NH = \frac{{MN}}{2} = \frac{{10}}{2} = 5cm;\) \(OH = O'H = \frac{{OO'}}{2} = \frac{{24}}{2} = 12cm\) Áp dụng định lý Pythagore trong tam giác vuông OMH: \(OM = R = \sqrt {M{H^2} + O{H^2}} = \sqrt {{5^2} + {{12}^2}} = 13\)cm. Đáp án B.
|