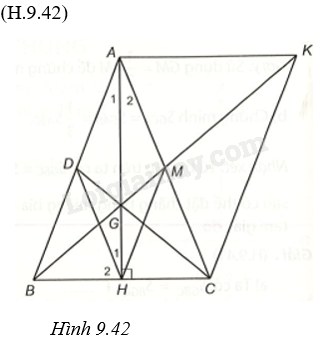
Giải bài 5 trang 85, 86 vở thực hành Toán 7 tập 2

Đề bài

Cho tam giác ABC cân tại A, đường cao AH $\left( {H \in BC} \right)$.

a) Chứng minh $\Delta AHB = \Delta AHC$.

b) Từ H kẻ đường thẳng song song với AC, cắt AB tại D. Chứng minh $AD = DH$.

c) Gọi M là trung điểm của AC, CD cắt AH tại G. Chứng minh ba điểm B, G, M thẳng hàng.

d) Chứng minh chu vi $\Delta ABC$ lớn hơn $AH + 3BG$.

Lời giải chi tiết

a) Xét hai tam giác vuông $\Delta AHB$ và $\Delta AHC$ có:

AH chung, $AB = AC$nên $\Delta AHB = \Delta AHC$ (cạnh huyền – cạnh góc vuông).

b) Từ câu a) $\Delta AHB = \Delta AHC$, suy ra $\widehat {{A_1}} = \widehat {{A_2}}$ (hai góc tương ứng).

Ta có AC//HD, suy ra $\widehat {{H_1}} = \widehat {{A_2}}$ (so le trong), từ đó $\widehat {{A_1}} = \widehat {{H_1}}$ nên $\Delta$ADH cân tại D, suy ra $AD = DH$. (1).

c) Ta có $\widehat {{A_1}} + \widehat {ABC} = {90^o}$ (vì tam giác AHB vuông tại H), $\widehat {{H_1}} + \widehat {{H_2}} = \widehat {AHB} = {90^o}$ (vì AH vuông góc với BC tại H). Vì $\widehat {{A_1}} = \widehat {{H_1}}$ nên $\widehat {ABH} = \widehat {{H_2}}$, suy ra tam giác BHD cân tại D, do đó $BD = DH$. (2).

Từ (1) và (2) suy ra D là trung điểm của AB.

Tam giác ABC có CD, AH là hai trung tuyến cắt nhau tại G nên G là trọng tâm tam giác ABC.

Khi đó, BG là trung tuyến, M là trung điểm của AC nên BG đi qua M, tức B, G, M thẳng hàng.

d) Trên tia BM lấy điểm K sao cho M là trung điểm của BK, khi đó $2BM = BK$.

Vì G là trọng tâm của tam giác ABC nên $3BG = 2BM$. Từ đó $BK = 2BM = 3BG$.

Ta chứng minh được $\Delta BMC = \Delta KMA\left( {c.g.c} \right)$, suy ra $BC = AK$.

Trong tam giác ABK, ta có:

$AK + AB > BK$ hay $BC + AB > BK$, mà $BK = 2BM = 3BG$ nên $BC + AB > 3BG$. (3)

Trong tam giác vuông AHC, ta có $AC > AH$. (4)

Từ (3) và (4) suy ra $BC + AC + AB > AH + 3BG$.