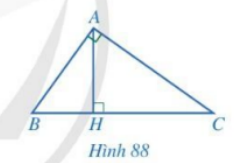
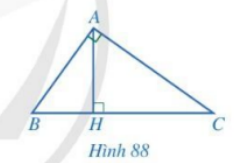
Giải bài 5 trang 85 SGK Toán 8 – Cánh diềuCho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh: Đề bài Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh: a) \(\Delta ABC \backsim \Delta HBA\) và \(A{B^2} = BC.BH\) b) \(\Delta ABC \backsim \Delta HAC\) và \(A{C^2} = BC.CH\) c) \(\Delta ABH \backsim \Delta CAH\) và \(A{H^2} = BH.CH\) d) \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Chứng minh các cặp tam giác đồng dạng rồi suy ra tỉ số đồng dạng tương ứng. Lời giải chi tiết
a) Xét tam giác ABC và tam giác HBA có: \(\widehat {BAC} = \widehat {BHA} = 90^\circ ;\,\,\widehat B\) chung \( \Rightarrow \Delta ABC \backsim \Delta HBA\) (g-g) \( \Rightarrow \frac{{AB}}{{HB}} = \frac{{BC}}{{BA}} \Rightarrow A{B^2} = BC.HB\) b) Xét tam giác ABC và tam giác HAC có: \(\widehat {BAC} = \widehat {AHC} = 90^\circ ;\,\,\widehat C\) chung \( \Rightarrow \Delta ABC \backsim \Delta HAC\) (g-g) \( \Rightarrow \frac{{AC}}{{HC}} = \frac{{BC}}{{AC}} \Rightarrow A{C^2} = BC.CH\) c) Ta có: \(\Delta ABC \backsim \Delta HBA\) và \(\Delta ABC \backsim \Delta HAC\) nên \(\Delta ABH \backsim \Delta CAH\) \( \Rightarrow \frac{{AH}}{{CH}} = \frac{{BH}}{{AH}} \Rightarrow A{H^2} = BH.CH\) d) Ta có: \(A{B^2} = BC.BH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.BH}}\) \(A{C^2} = BC.CH \Rightarrow \frac{1}{{A{B^2}}} = \frac{1}{{BC.CH}}\) \(A{H^2} = BH.CH \Rightarrow \frac{1}{{A{H^2}}} = \frac{1}{{BH.CH}}\) \(\begin{array}{l} \Rightarrow \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{BC.BH}} + \frac{1}{{BC.CH}}\\ = \frac{1}{{BC}}.\left( {\frac{1}{{BH}} + \frac{1}{{CH}}} \right)\\ = \frac{1}{{BC}}.\frac{{BH + CH}}{{BH.CH}}\\ = \frac{1}{{BC}}.\frac{{BC}}{{BH.CH}}\\ = \frac{1}{{BH.CH}}\\ = \frac{1}{{A{H^2}}}\end{array}\)
|