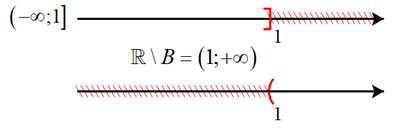Giải bài 52 trang 17 SBT toán 10 - Cánh diều

Đề bài

Cho các tập hợp: $A = \left[ { - 1;2} \right),B = \left( { - \infty ;1} \right]$

Xác định $A \cap B;A \cup B;A\backslash B;B\backslash A;\mathbb{R}\backslash B;{C_\mathbb{R}}A.$

Lời giải chi tiết

a)

Vậy $A \cap B = \left\{ {x \in \mathbb{R}\left| { - 1 \le x < 2,x \le 1} \right.} \right\} = \left\{ {x \in \mathbb{R}\left| { - 1 \le x \le 1} \right.} \right\} = \left[ { - 1;1} \right]$

b)

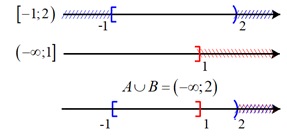
Vậy $A \cup B = \left\{ {x \in \mathbb{R}\left| { - 1 \le x < 2,x \le 1} \right.} \right\} = \left\{ {x \in \mathbb{R}\left| {x < 2} \right.} \right\} = \left( { - \infty ;2} \right)$

c)

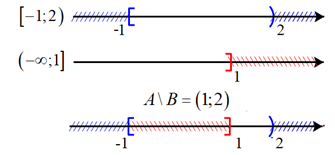
Vậy $A\backslash B = \left\{ {x \in \mathbb{R}\left| { - 1 \le x < 2} \right.} \right\}\backslash \left\{ {x \in \mathbb{R}\left| {x \le 1} \right.} \right\} = \left\{ {x \in \mathbb{R}\left| {1 < x < 2} \right.} \right\} = \left( {1;2} \right)$

d)

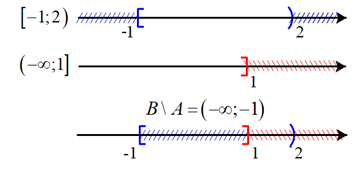
$B\backslash A = \left\{ {x \in \mathbb{R}\left| {x \le 1} \right.} \right\}\backslash \left\{ {x \in \mathbb{R}\left| { - 1 \le x < 2} \right.} \right\} = \left\{ {x \in \mathbb{R}\left| {x <  - 1} \right.} \right\} = \left( { - \infty ; - 1} \right)$

e)

Vậy $\mathbb{R}\backslash B = \mathbb{R}\backslash \left\{ {x \in \mathbb{R}\left| {x \le 1} \right.} \right\} = \left\{ {x \in \mathbb{R}\left| {x > 1} \right.} \right\} = \left( {1; + \infty } \right)$

g)

Vậy ${C_\mathbb{R}}A = \mathbb{R}\backslash \left\{ {x \in \mathbb{R}\left| { - 1 \le x < 2} \right.} \right\} = \{ x \in \mathbb{R}\left| {x <  - 1} \right.$ _hoặc $x \ge 2\}  = \left( { - \infty ; - 1} \right) \cup \left[ {2; + \infty } \right)$