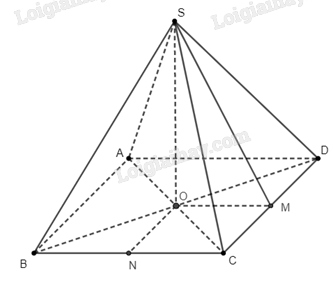
Giải bài 57 trang 118 sách bài tập toán 11 tập 2 - Cánh diềuCho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a\), \(O\) là hình chiếu Đề bài Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a\), \(O\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\), \(SO = a\). Gọi \(M\) là hình chiếu của \(O\) trên \(CD\) (xem hình dưới). a) Đường thẳng \(AC\) vuông góc với mặt phẳng nào trong các mặt phẳng sau đây? A. \(\left( {SAB} \right)\) B. \(\left( {SAD} \right)\) C. \(\left( {SBC} \right)\) D. \(\left( {SBD} \right)\) b) Số đo của góc nhị diện \(\left[ {A,SO,M} \right]\) bằng: A. \({30^o}\) B. \({45^o}\) C. \({135^o}\) D. \({150^o}\) c) Khoảng cách giữa hai đường thẳng \(SO\) và \(BC\) bằng: A. \(a\) B. \(\frac{a}{2}\) C. \(\frac{{a\sqrt 2 }}{2}\) D. \(\frac{{a\sqrt 3 }}{2}\) d) Thể tích của khối chóp \(S.ABCD\) bằng: A. \({a^3}\) B. \(\frac{{{a^3}}}{2}\) C. \(\frac{{{a^3}}}{3}\) D. \(3{a^3}\) e) Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SOM} \right)\) bằng: A. \(a\) B. \(\frac{a}{2}\) C. \(\frac{{a\sqrt 2 }}{2}\) D. \(\frac{{a\sqrt 3 }}{2}\) g) Côtang của góc giữa đường thẳng \(SM\) và \(\left( {ABCD} \right)\) bằng: A. \(\frac{1}{2}\) B. \(2\) C. \(1\) D. \(\frac{{\sqrt 5 }}{5}\) Phương pháp giải - Xem chi tiết a) Sử dụng kiến thức về đường thẳng vuông góc với mặt phẳng b) Xác định góc phẳng nhị diện của góc nhị diện \(\left[ {A,SO,M} \right]\). c) Xác định đường vuông góc chung của hai đường thẳng \(SO\) và \(BC\). d) Công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\), với \(S\) là diện tích đáy và \(h\) là chiều cao của khối chóp đó. e) Chứng minh rằng \(M\) là hình chiếu của \(C\) trên \(\left( {SOM} \right)\), từ đó khoảng cách cần tính là đoạn thẳng \(CM\). g) Xác định góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\), rồi tính côtang của góc đó. Lời giải chi tiết
a) Do \(S.ABCD\) là hình chóp tứ giác đều, ta suy ra \(ABCD\) là hình vuông. Điều này suy ra \(AC \bot BD\). Hơn nữa, do \(SO \bot \left( {ABCD} \right)\) nên \(SO \bot AC\). Như vậy, do \(AC \bot BD\), \(SO \bot AC\) nên \(AC \bot \left( {SBD} \right)\) Đáp án đúng là D. b) Do \(SO \bot \left( {ABCD} \right)\), ta suy ra \(SO \bot AO\) và \(SO \bot OM\). Do đó, góc \(\widehat {AOM}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SO,M} \right]\). Do \(M\) là trung điểm của \(CD\), và tam giác \(COD\) vuông cân tại \(O\), ta suy ra \(\widehat {MOD} = {45^o}\) và \(OM \bot CD\). Do đó \(\widehat {AOM} = \widehat {AOD} + \widehat {MOD} = {90^o} + {45^o} = {135^o}\). Vậy số đo của góc nhị diện \(\left[ {A,SO,M} \right]\) là \({135^o}\). Đáp án đúng là C. c) Gọi \(N\) là trung điểm của \(BC\). Tam giác \(OBC\) vuông cân tại \(O\), nên ta có \(ON \bot BC\). Hơn nữa, do \(SO \bot \left( {ABCD} \right)\), nên \(SO \bot ON\). Vậy \(ON\) là đường vuông góc chung của \(SO\) và \(BC\), do đó khoảng cách giữa hai đường thẳng \(SO\) và \(BC\) là đoạn thẳng \(ON\). Dễ dàng chứng minh được \(ON = \frac{1}{2}AB = \frac{a}{2}\), vậy khoảng cách giữa hai đường thẳng chéo nhau \(SO\) và \(BC\) bằng \(\frac{a}{2}\). Đáp án đúng là B. d) Thể tích khối chóp \(S.ABCD\) là \(V = \frac{1}{3}Sh = \frac{1}{3}A{B^2}.SO = \frac{1}{3}{a^2}.a = \frac{{{a^3}}}{3}\). Đáp án đúng là C. e) Do \(SO \bot \left( {ABCD} \right)\), ta suy ra \(SO \bot CM\), mà theo câu b, ta suy ra \(CM \bot OM\). Từ đó ta có \(CM \bot \left( {SOM} \right)\). Như vậy \(M\) là hình chiếu của \(C\) trên \(\left( {SOM} \right)\), từ đó khoảng cách từ \(C\) đến \(\left( {SOM} \right)\) là đoạn thẳng \(CM\). Do \(CM = \frac{1}{2}CD = \frac{a}{2}\), nên khoảng cách từ \(C\) đến \(\left( {SOM} \right)\) bằng \(\frac{a}{2}\). Đáp án đúng là B. g) Do \(O\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\), ta suy ra góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\) là góc \(\widehat {SMO}\). Ta có \(\cot \widehat {SMO} = \frac{{OM}}{{SO}} = \frac{{\frac{a}{2}}}{a} = \frac{1}{2}\). Vậy côtang của góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(\frac{1}{2}\). Đáp án đúng là A.
|