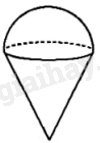
Giải bài 8 trang 127 vở thực hành Toán 9 tập 2Một chiếc kem ốc quế gồm hai phần: Phần phía dưới là một hình nón có chiều cao gấp đôi bán kính đáy, phần trên là một nửa hình cầu có đường kính bằng đường kính đáy của hình nón phía dưới. Thể tích phần kem phía trên bằng (200c{m^3}). Tính thể tích của cả chiếc kem. Đề bài Một chiếc kem ốc quế gồm hai phần: Phần phía dưới là một hình nón có chiều cao gấp đôi bán kính đáy, phần trên là một nửa hình cầu có đường kính bằng đường kính đáy của hình nón phía dưới. Thể tích phần kem phía trên bằng \(200c{m^3}\). Tính thể tích của cả chiếc kem.
Phương pháp giải - Xem chi tiết + Ta có \({V_1} = \frac{1}{2}.\frac{4}{3}\pi {R^3} = 200\left( {c{m^3}} \right)\), từ đó tính được R. + Tính thể tích của phần kem phía dưới. + Thể tích chiếc kem bằng tổng thể tích phía trên và phía dưới chiếc kem. Lời giải chi tiết Thể tích phần kem phía trên là \(200c{m^3}\) nên: \({V_1} = \frac{1}{2}.\frac{4}{3}\pi {R^3} = 200\left( {c{m^3}} \right)\), suy ra \(R = \sqrt[3]{{\frac{{300}}{\pi }}}cm\). Thể tích phần kem phía dưới là: \({V_2} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {R^2}.2R \\= \frac{2}{3}\pi {R^3} = \frac{2}{3}\pi .\frac{{300}}{\pi } = 200\left( {c{m^3}} \right).\) Thể tích cả chiếc kem là: \(200 + 200 = 400\left( {c{m^3}} \right)\).
|